This is just a WIP, but I’m posting it because who knows when I’ll have time to post again and because hopefully I can get some feedback on my math / script.
I’ve been working through the Dessler 2010 paper in Science, “A Determination of the Cloud Feedback from Climate Variations over the Past Decade”. It was highlighted in a post at RealClimate.
The script and data that I’m working with is available here. The NC file I’ve included is what I downloaded from the CERES website to try and match what was used in the Dessler10 paper: SSF1deg, with a spatial resolution of “global mean”, the data from the Terra satellite, and the full available time range. The NC file includes more, but all I’ve used is the Net, SW, and LW Flux for both Clear Sky and All Sky.
In order to read the NC file in R, you’ll need to install the ncdf package if you haven’t already.
Anyhow, here is the graph from my script when attempting to reproduce Figure 1 in the paper:
Comparing this with the actual figure in the paper shows that they are pretty close:
Obviously, I haven’t tried to reproduce the figure exactly. For one, I haven’t made the adjustments to get from CRF to R_cloud anomalies, as this would seem to require significantly more effort using the reanalysis system. Furthermore, I have calculated CRF using simply the CERES estimates of R_all-sky and R_clear-sky rather than the R_clear-sky obtained from the reanalysis system. The paper notes that “the differences between CRF and R_cloud are small for these data”, and I take this to mean that our results should not depend too heavily on the changes there. Finally, my temperature anomalies are simply those of GISS, HadCRUT, and NOAA, rather than from the reanalysis system.
There are definitely differences between the middle figures in the charts, which is to be expected based on the slightly different calculation. However, what I’m a bit stumped on are the differences in the top graph. This should be relatively straightforward graphing of the data and calculating monthly anomalies, and given that we’re using the same data I would expect it to be identical, but there are slight differences – most obviously in the first few months of 2010.
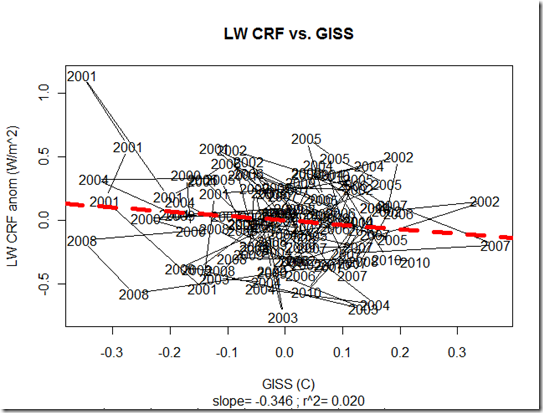
Anyhow, using GISS temps and the aforementioned CRF, I get quite a different result:
This corresponds to a fairly strong negative cloud feedback (-0.892 W/m^2/K, with the 2.5%-97.5% confidence interval (from the simple OLS regression) of [-1.602, -0.18] including the strong negative feedbacks that were originally excluded by the paper. Furthermore, we get a r^2 value of 5% compared to the 2% value in the paper.
It is quite possible that I’ve screwed up the analysis somehow. For one, it is possible that I’ve got the sign inverted for the CRF anomaly. I’m pretty sure it is correct, however, as I use r_clr-sky minus r_all-sky, which is on average 18 W/m^2 here. I multiple by –1 (same thing as just doing r_all-sky minus r_clr-sky, but I keep it consistent with the paper by doing the subtraction the other way) to get the average cloud forcing (which we know to be negative). Furthermore, the peaks and troughs seem to match up fairly well in my middle chart versus that in Dessler 2010.
There is also the difference I mentioned before, where I use r_clr-sky based on the CERES observations rather than a calculated value from reanalysis. Dessler10 mentions that he does the opposite because of bias in the measurements: “And, given suggestions of biases in measured clear-sky fluxes (22), I chose to use the reanalysis fluxes here.” The paper referenced there is Sohn and Bennartz in JGR 2008, “Contribution of water vapor to observational estimates of longwave cloud radiative forcing. However, that paper only refers to bias in the clear-sky LW radiation calculations. A quick look at only LW and SW separately gives the following result: (NOTE: if you’re using the lw or sw variables in this scenario, keep in mind those are given in the opposite direction to those of the net variable, since they are outgoing fluxes).
Note that the stronger negative feedback comes from the increase in reflected SW radiation, so even if our LW result is affected by measurement bias, the SW negative feedback is stronger than any SW negative feedback represented in the models shown in Dessler10 (and indeed, only 3 of the 10 models shown have a negative SW component).
But I’m doubtful that the LW result should be discounted based on measurement bias anyhow. For one, the SB08 paper refers to bias in the absolute calculation of CRF, not necessarily to the change in CRF, and the effect is minimal there (around 10% of only the OLR). Second, the bias should affect it in the opposite direction – it would make the cloud feedback appear more positive, not negative. From the SB08 paper, they mention: “As expected, OLR fluxes determined from clear-sky WVP are always higher than those from the OLR with all-sky OLR (except for the cold oceanic regions) because of drier conditions over most of the analysis domain.” Obviously, clear-sky days don’t prevent as much OLR from leaving the planet as cloudy days, and SB08 estimates that about 10% of this effect is from water vapor instead of all of it being from clouds. So, warmer temperatures should increase water vapor, which will be more prevalent on the cloudy days vs. the clear sky days, which in turn will make it appear that clouds are responsible for trapping more OLR than they actually do. In other words, the bias includes some of the positive feedback due to water vapor – which is already counted elsewhere – in the estimation of cloud feedback. Thus, if we are to take into account the bias, we have slightly underestimated the magnitude of the negative cloud feedback.
The final difference I should mention is the process of converting from CRF to the r_cloud in Dessler10 using the reanalysis system. As the Dessler paper mentions, and the chart bears out, however, the differences are quite small between these two quantities – that they should result in the transformation from the estimate negative feedback seen here to the positive one would be surprising to me.
I’ll end by noting that repeating the analysis with other temperature indices did not yield as significant of results. I repeated it with HadCRUT, NOAA, and then an average of all three indices. The table below shows the results:
| Dataset | Slope (w/m^2/k) | 2.5%-97.5% | r^2 |
| Giss | -0.8922 | [-1.602,-0.18] | .0499 |
| HadCRUT | -0.3999 | [-1.37, .57] | .0056 |
| NOAA | -0.5964 | [-1.50, .31] | .0142 |
| Average | -0.7618 | [-1.62, .13] | .024 |
In each scenario, however, using OLS regression yields an estimated negative cloud feedback.
I am quite surprised by these results, given their contradiction with those in Dessler10. I lean towards thinking I’ve made some mistake, particularly since my analysis – based only on CERES satellite data and surface temperatures – is simple and relatively straight-forward, to the point where I would have expected someone else to have already done it.
Update (8/1)
I’ve gotten a chance to read up on this a good deal more, and the method of calculating the change in CRF due to temperature is straight-forward and should be correct. However, after playing with the data in figure 1B, it is clear that the modifications to fluxes to remove the non-cloud impact (converting from CRF to R_cloud) can have a substantial impact on the resulting calculation for actual cloud feedback. Based on the modifications made in the Dessler paper, it seems that the resulting sign of the short-term cloud feedback depends on the surface temperature dataset chosen. Interestingly, the satellite temperature indices both yield the highest correlation and the more negative cloud feedbacks. I will post more on this, and am currently downloading the radiative kernel and reanalysis data necessary to perform the flux adjustments myself.