New page on the observation-based estimate of climate sensitivity

You may have noticed my new page, which can be accessed on the right.  I created this because I’ve been posting often lately on the method originally introduced in Forster and Gregory (2006), which has led to the recent disagreement between the latest Dessler and Spencer papers.  I will simply link to this page in future posts so that readers can find the relevant history, papers, and resources, rather than burdening each post on this topic with the same links/introductions.

Estimated Sensitivity and Climate Response with TLS

As discussed in a previous post, Forster and Gregory (2006) and Murphy et. al. (2009) use OLS regressions of temperatures versus the difference between measured TOA flux and known/estimated forcings to try and determine the overall climate feedback.  As the inverse of this feedback is assumed to be the climate sensitivity, any underestimate in this climate feedback will hence lead to an overestimate in the climate sensitivity from this method.

Now, one possible issue with the method is that there are measurement errors in the monthly temperature anomalies, and OLS will lead to underestimates of the regression coefficient when there are errors in the independent variable.  A possible way to combat this regression attenuation is to use total least squares, which fits the line considering errors in the independent variable as well.  Of course, the trouble with using this method is that you need to have some idea of the relative variance of the “errors”, otherwise you could swing the opposite direction and get a huge overestimate. 

As I don’t have a strong statistics background, implementing this Deming regression (a simple, specialized case of TLS) is rather new to me.  However, one thing that is clear is that the assumed value for δ – the ratio of variance of errors in the dependent variable over the variance of errors in the independent variable – greatly affects the resulting estimate.  Below, I show the Deming regression estimates for the overall feedback response (lambda, or Y, the inverse of sensitivity) based on the  assumed δ.  I use the HadCRUT3 and GISS datasets and the CERES net TOA flux measurements from March 2000 through December 2010 (the length of the CERES dataset):

 

Using OLS, which assumes no errors in the independent variable (or a δ = infinity), yields climate feedbacks of 1.16 and 1.19 W/m^2/K for GISS and HadCRUT respectively (equal to a sensitivity of around 3.2 C).

The red lines in the posts above correspond to δ = variance in Q-N divided by the variance in temperatures.  There is no strong reason to suggest that this assumption is correct, but for reference, using the specified values for δ  would yield estimates of  5.10 and 6.77 W/m^2/K for the climate response in those temperature sets, corresponding to tiny values of 0.75 and 0.56 C for sensitivity. 

As Nic mentions in the comments of that last post, and Forster and Gregory (2006) note, the errors leading to the low correlation are not necessarily coming from measurement errors, but rather from other radiative influences.  However, it appears that even if we assume the variance of errors in Q-N is much larger (say, 75x) than that of variance of errors due to uncertainty in monthly temperature anomalies, the effect is still quite noticeable (about 2.5x the climate feedback estimated in HadCRUT, 1.5x in GISS).  In fact, if we assume the 0.075 C for the 1 sd in the monthly temperature errors, and then use the variance of Q-N itself as an upper bound on its possible errors, that 75x is what we get. 

I should note that Murphy et. al. (2009) also uses orthogonal regressions for comparison, and these (predictably) lead to higher estimates of the response, though lower than I would expect based on my tests.  At the moment, however, I’m not able to reproduce the lower results using this orthogonal distance regressions (which is basically the Deming regression above but with δ = 1, although they likely adjusted for units as well).  They make a case on the grounds of cause and effect why OLS is more appropriate (surface temperature influence radiative flux at 0 time lag more than the opposite), and certainly it would seem that assuming the same errors in both variables is probably incorrect, but I fail to see why this means that we should not necessarily take into account ANY of the measurements errors in T, particularly when the errors on a monthly scale seem large relative to the monthly anomalies themselves.  Of course, as I mentioned above, I am still in the process of learning these methods.

Anyhow, the script for this post is available here.

Measuring Sensitivity using the FG06 method with a GFDL CM2.1 control run

I originally posted on the Forster and Gregory 2006 method for determining climate sensitivity back in June.  Since then, I’ve come across a number of issues (mostly discovered by others) on why this method may not constrain the sensitivity with the accuracy previously assumed.  I will likely need to create a page of resources on this alone, because the number of links to blog posts and papers could easily grow unmanageable if I were to repeat them in every post.  However, for now I’ll mention the recent Science of Doom and Isaac Held  posts, and then begin listing some of the difficulties I see (particularly without using a limited time period):

1. The unknown radiative forcing.  This is Dr. Spencer’s main objection (SB08, SB10, and part of SB11), which suggests the forcing will lead to an underestimate of the response (and hence and overestimate of sensitivity) if it is correlated with T.  Murphy and Forster 2010 argue that the effect is small, but it doesn’t look like their use of such a deep mixed layer was appropriate.  Science of Doom has a good introduction to this issue in the post I link to above.
2. There is not a strong reason to believe that the radiative response to a temperature change is both constant across all seasons and linear (also briefly mentioned in the SoD post).  However, it theoretically could be a reasonable approximation.
3. Dessler 2010 concludes that there is unlikely to be a correlation between the short-term/instantaneous cloud feedback and the long-term cloud feedback (at least, it’s not present in models).  The set-up of FG06 implicitly only includes the short-term feedback, and since the cloud feedback is one of the biggest uncertainties surrounding equilibrium climate sensitivity, it suggests that the FG06 method could not necessarily  diagnose the ECS in this case.
4. There is a timing offset between the sea surface temperature changes and the bulk of the tropospheric temperature changes (1 – 3 months).  When using a smaller period with interannual variations greater than the long-term trend (e.g., the CERES era), and with the bulk of the Planck response coming from the atmosphere, the timing offset would lead to an underestimate of the response.
5. Using the method in the control runs of models generally leads to a large overestimate of the climate sensitivity (which suggests major issues with the method, the models, or both).
6. Errors in the surface temperature measurements will yield underestimates of the response (and overestimates in the sensitivity).  I specifically point to the surface temperature measurements rather than the satellite flux measurements because they act as the independent variable in the regressions, meaning they’ll lead to regression attenuation using traditional OLS methods (assuming Gaussian white noise for the flux measurements, we would get a lower correlation but not necessarily an underestimate).
7. The sampling error using only (for example) 10 year periods could make it difficult to diagnose accurately.

For this post, I will briefly mention #5, and then use the GFDL 2.1 500 year control run from PCMDI to explore #6 and #7.

General Inaccuracies using the GCM Control Runs

For point #5, I will point to a perhaps unexpected place…figure 2 of Dessler 2011:

The black lines are from the control runs of the models.  Note the regression slopes at 0 lag (which corresponds to the FG06 method), which I’ve circled in green.  Now, the average ECS of these models we know to be about 3 K, which corresponds to a radiative response of about (3.8 W/m^2 / 3 K) =  1.27 W/m^2/K for the radiative response, a number that we’d expect to see as the average regression slope.  But instead, the average regression slope is closer to 0.5 W/m^2/K, which corresponds to a whopping 7.6 K ECS, more than double of what is known for these models.  Using the FG06 method in the control runs of the models thus overestimates the sensitivity in what appears to be 12 out of the 14 models.   Dr. Spencer goes into some more issues of testing this against models.

Anyhow, there appear to be two models that actually show reasonable results when using the FG06 method.  From the Trenberth, Fasullo, and Abraham response, it appears that one of them is ECHAM_MPI.  The other one looks to be GFDL CM2.1 from my tests:

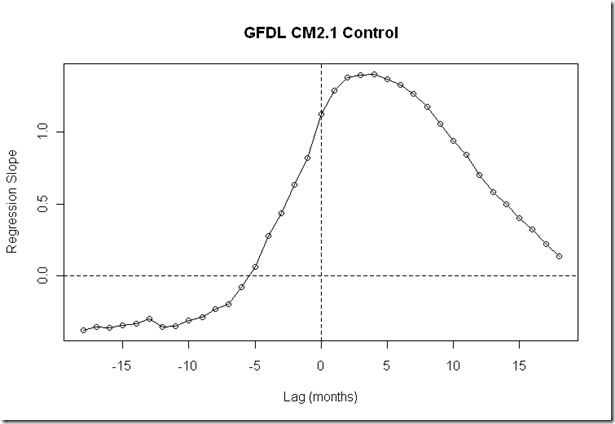
Closer Look at the GFDL CM2.1 Control Run

The GFDL CM2.1 has a ECS of 3.4 according to the IPCC AR4 table.  This corresponds to a response of 1.12 W/m^2/K, which is almost the exact value I get when using the 500 years of the control run and monthly temperature anomalies (r^2=.09).  Of course, it is curious why the correlation would be so low if the FG06 method uses an appropriate model, considering there is no measurement noise in the flux or temperature outputs from the model.

Anyhow, before continuing further, I’d like to show a chart of the control run global surface air temperature, which has got me scratching my head a bit:

Now, my understanding is that the pre-industrial control experiment does not include any change in forcings, and that the model is run to “stabilize” prior to the start of the control experiment.  The gray lines are the monthly anomalies, while the black line is the 30 year moving average.  Note that we see climate-scale trends (using the 30 year averages) that are completely unforced (if I’m understanding it correctly); this is not “natural variability” in terms of solar or volcanic variation, but rather in the “no TOA forcing changes” sense.  Whether this is simply model drift, or is actually supposed to be simulating long-term, unforced variability, I’m not sure…it’s on the scale of 0.2C for what appears to be some < 75 year periods, which seems like it could be significant compared to the 20th century rise.

Anyhow, I will proceed with some different trials in order to diagnose the climate feedback in the model’s control run and compare it to the known value.  First, I’ll note that using annual averages over the 500 year period gives me a response of 1.37 W/m^2/K (r^2 = 0.26), which would be an underestimate of sensitivity.  Dr. Held, in his response to my comment on his blog, mentioned that using 1000 years (which I don’t think was available at PCMDI), he got  response of 1.7 W/m^2/K.  I was a bit surprised not to match his results, since 500 years seems like it would be enough to constrain it, until I broke it down into two 250 years periods and found responses of 1.56 and 1.7 W/m^2/K, which seems to suggest that there are periods of temperature change that are not met with corresponding radiative responses (perhaps this is what allows for the continuing drift?).

Using Absolute Values Rather Than Anomalies

Anyhow, in Murphy et. al 2009, they extend the FG06 method to use CERES monthly observations.  One curious point is that in figure 2, they use interannual AND seasonal variations (that is, they don’t take monthly anomalies) to show the radiative response.  Steve McIntyre has explored this as well.  The result is that you get higher r^2 values, but I think this may inflate the confidence we should have in the Murphy (2009) method.  After all, it doesn’t seem that seasonal changes in temperature and the radiative response would necessarily be equal to longer term changes, and in fact using absolute values for monthly temperature anomalies and fluxes with the 500 year control run results in a  response of 4.55 W/m^2/K (way higher than the known long-term value) with a r^2 = 94%!  However, that 94% clearly is not indicative that it is accurately reflecting the ECS.  Of course, such a high value may only suggest that the GFDL CM2.1 model overestimates the flux response to seasons, or underestimates the seasonal temperature response.

 

Regression Attenuation from Uncertainty in Surface Temperatures

I added white noise with a standard deviation of .075 C into the surface air temperatures to simulate measurement/sampling noise, based on estimates of the uncertainty presented in the charts of the HadCRUTv3 paper towards the early 21st century (during the CERES era).  This resulted in the expected regression attenuation in the 500 year monthly test, bringing the estimated response down to about 1.02 W/m^2/K, and thus yielding a slight overestimate of the sensitivity.  It is curious that the use of TLS to avoid this attenuation is not examined in more detail.  For instance, FG06 mention:

For less than perfectly correlated data, OLS regression of Q-N against T_s will tend to underestimate Y values and therefore overestimate the equilibrium climate sensitivity (see Isobe et al. 1990).

The reason main reasons that they give for sticking with OLS is two-fold: 1) the issue of cause and effect (T_s inducing the radiative flux changes at short time scales, not the opposite), also discussed in MF09, which is in dispute by Spencer in point #1 of the post, and 2) that using it on the model HadCM3 does not yield accurate results using different regressions.

I will point out that even IF no unknown radiative forcing is confounding the feedback signal in this way, this still does NOT mean that there is no “error” in the independent variable…as shown above, HadCRUTv3 includes estimates of uncertainties.  Furthermore, that another method correcting for these errors (both in terms of cause and effect and measurement error) would yield overestimates of the response in a climate model that includes neither these specified variations in cloud forcing nor measurement error is unsurprising, but it says nothing about whether a different regression method is appropriate for real world data that DOES include such errors.  Finally, I found the following statement from FG06 appendix quite interesting:

Another important reason for adopting our regression model was to reinforce the main conclusion of the paper: the suggestion of a relatively small equilibrium climate sensitivity. To show the robustness of this conclusion, we deliberately adopted the regression model that gave the highest climate sensitivity (smallest Y value).  It has been suggested that a technique based on total least squares regression or bisector least squares regression gives a better fit, when errors in the data are uncharacterized (Isobe et al. 1990). For example, for 1985–96 both of these methods suggest YNET of around 3.5 +.- 2.0 W/m^2/K (a 0.7–2.4 K equilibrium surface temperature increase for 2 x CO2), and this should be compared to our 1.0–3.6-K range quoted in the conclusions of the paper.

Murphy et. al (2009) explore orthogonal regression a bit as well, but I couldn’t find anything that explicitly takes into account the known uncertainties in the surface temperatures.

 

Sampling Error in 10 year intervals

Finally, I will look at the different estimates we get for the climate radiative response when breaking the 500 year control run into 50 10-year periods (and still including noise).  I set the standard deviation for Net TOA flux measurements to 0.33 W/m^2 per month when adding in the white noise (based on estimated CERES RMSE (SW + LW) / sqrt(2)) The red lines represent the “true” radiative response.  Using monthly values, we get the following results over 10 year periods:

Based on those responses, this includes climate sensitivities from 1.7 C to 14.2 C (!) based on a 10-year period, when the known sensitivity is 3.4 C.

For annual data (which should reduce some of the measurement noise, but yield a smaller sample size), we get:

Which includes everything from 0.8 C to 13.1 C.

Interestingly, these sampling errors tend to lead towards overestimates of the response, or underestimates in climate sensitivity.  I’m not quite sure at the moment why this should be the case.

All code and data for this post is available here.