1. Introduction
This post should be the first in a series covering how we might derive an "empirical" estimate for climate sensitivity from ocean heat content (OHC) and surface temperature changes. I’ve touched on this topic a few times in previous posts, but my goal for this one is to have it be a more thorough examination.
The basic equation I want to use here is one we’ve seen quite a few times before:
ΔN = ΔF + λ*ΔT
Here, N is the TOA radiative flux, F is the forcing, T is the surface temperature, and λ is the radiative response term, also referred to as "effective sensitivity" in Soden and Held (2006) and "climate feedback parameter" in Forster and Gregory (2006), both of which can be confusing as they mean slightly different things than "sensitivity" and "feedback" in current climate lexicon. For more information you can see my page here, although I think parts of that may out-of-date enough to not totally reflect my evolving views. For instance, I see more and more evidence that this radiative response to inter-annual fluctuations is a poor predictor of the radiative response on the climate scale. This is why I hope to use differences in longer periods — e.g. 30 years — to determine a more relevant value for λ. Of course, we don’t have a single satellite that runs that long to compare TOA imbalance, but we can estimate it…from the OHC data.
One other thing worth mentioning here is that while theoretically it should be possible to determine the equilibrium climate sensitivity (temperature change with a doubling of CO2) by simply dividing the forcing (~3.7 W/m^2) by the radiative response, this assumes that λ is a constant for different timescales and forcing magnitudes, which is far from true in some models (whether this departs significantly from constant in the "real world" system is debatable). Winton et al. (2010) refer to this in terms of "Ocean Heat Uptake Efficacy", and Isaac Held has a discussion of it on his blog. . Paul_K also discussed this at The Blackboard. This is why the dividing the CO2 forcing by "effective sensitivity" in Soden and Held (2006) calculated from 100 years of the A1B scenario does not directly match the equilibrated temperature change from the idealized CO2x2 scenario. While the latter may be near impossible to accurately determine without thousands of years of well-constrained observations, the former is arguably much more useful anyhow, so I’ll set my sights on that.
2. Forcing Uncertainty
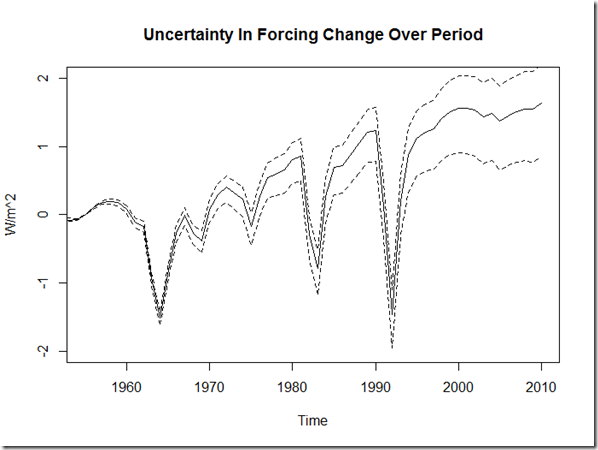
The start of the NOAA OHC data is 1955, so estimating the TOA imbalance from this data means we’re limited to 1955 and on (actually a bit later, but we’ll discuss that in the next section). So, what kind of forcing uncertainty are we looking at over this period? For this, we can first take a look at the GISS forcings, derived in the method described from Hansen et al. (2005), which are also very similar to the AR4 time evolution of forcings modeled using MIROC+SPRINTARS. Similarly, I digitized the GFDL CM2.1 forcing evolution from Held et al. (2010), and we get something similar. Moreover, since the emissions histories are all very similar, it seems the differences in these forcing histories can largely be determined based simply on an "aerosol efficacy factor" for anthropogenic aerosols. Here is a reconstruction of the GFDL CM2.1 forcing history from the GISS forcings, but using an "efficacy" of 0.75 for anthropegic aerosols:
As you can see, it is a pretty solid match. Thus, in order to determine the potential forcing histories used for “observations” in this experiment, I take the bounds for present-day aerosol estimates and compare that to the GISS forcing, and then use this factor for efficacy. The AR4 estimate for direct aerosol forcing is -0.5 +/- 0.4 W/m^2, and for indirect it is a most likely value of -0.7 W/m^2, with 5% to 95% range of -0.3 to -1.8 W/m^2. . From 1955, this produces the following uncertainty bounds for forcings if we use an aerosol forcing from -0.4 to -2.3 W/m^2:
With Monte Carlo, we can use a Gaussian distribution for the direct aerosol forcing and a triangle distribution for the indirect effect to get the following distribution for combined aerosol forcing difference (1955 – present day):
3. Inferred TOA Imbalance
As the measurements are very sparse down to 2000m prior to 2005, Levitus et al. (2012) provides only pentadal averages for OHC in the 0-2000m depths over that time period. We can calculate the approximate 5 year average TOA imbalance using the difference in 5 year OHC averages. For example, we estimate the 1957.5-1962.5 average TOA imbalance by subtracting the 1955-1959 average from the 1960-1964 average (the conversion from differenced Joules of 5 year averages to global average flux is ~0.124). However, we also need to note that not all of the extra energy is stored in the 0-2000m of the ocean…some goes into the atmosphere, into the cryosphere, or into the deeper ocean, so we’ll need to multiply this by some factor. We can use output from GCMs to estimate how well this method works:
First, for GISS-E2-R, a regression suggests only about 70% of the heat goes into this 0-2000m layer, but the reconstruction is quite good:
For GFDL CM2.1, the amount of heat is stored in 0-2000m ocean is about 85% of the imbalance, which seems more realistic. Levitus et al. (2012) estimates that 90% of the heat has gone into the ocean.
For a comparison of the 5 year running averages of OHC 0-2000m between the CMIP5 GFDL CM2.1 runs and the GISS-E2-R runs and the NOAA observations, I downloaded a bunch of ocean temperature data by layer from two different Earth System Grid Federation nodes: here and here. PLEASE NOTE: that this is NOT raw output data from the models, and it took a good amount of time on my part to download and process the data from the freely available kernel ocean temperatures into global heat content, so if you are using the data in the form I make available here (you can see the links in the scripts) I would request you acknowledge here as the source.
Additionally, NOAA provides 1 year averages for OHC 0-2000m from 2005.5-2011.5. By calculating the current imbalance using annual differences based on a regression dOHC/dT, we can estimate our imbalance up to the most recent full year.
4. Estimating Radiative Response Term using Monte Carlo
There are a number of uncertainties present, and to see their net effect I use Monte Carlo with 1000 iterations for each start year, from 1957 to 1985. The prior distribution for the forcing change was described in section 3. For estimating the heat going into the 0-2000m layer, I use a Gaussian distribution with standard deviation equal to the published standard error (from Levitus et al. 2012) for each year, with the OHC value for that year obviously centered on the most likely value presented in that data. This is then diff’d to determine the change in OHC, and converted into TOA imbalance by sampling from a uniform distribution that assumes 75%-85% of any heat imbalance is stored in that 0-2000m layer. Except for the “current” imbalance from 2005-2011, where the values are better constrained, I use 10-year averages (rather than 5) to limit the uncertainty for each start year.
Ultimately, the “radiative response” is determined from ((N2-N1)-(F2-F1))/(T2-T1), where N2 is the 2005-2011 Imbalance, N1 is the ten year average imbalance from an earlier start year period (starting at the StartYear), F2-F1 is the difference in forcing between the most recent 8 years and the average forcing over the earlier 10 year period, and T2-T1 is the difference in surface temperature between the most recent 8 years and the average surface temperature over the earlier 10 year period (the temperature used here is an average between the GISTemp and NCDC temperature datasets).
For those curious, the mean value I get for the TOA imbalance from 2005.5-2011.5 is ~0.57 W/m^2, which is pretty consistent with other estimates.
5. Results
The figure above shows the 2.5%-97.5% uncertainty (and median) for the observations, versus the span of 5 runs (and their median) for GISS E2-R and GFDL CM2.1. A few things jump out: first, the uncertainty for GISS E2-R is extremely small even compared to GFDL CM2.1, which we could probably attribute to an underestimate of internal variability. Second, that even though the error bars overlap for a number of periods, it would appear that these models underestimate the radiative response, suggesting that they likely overestimate climate sensitivity.
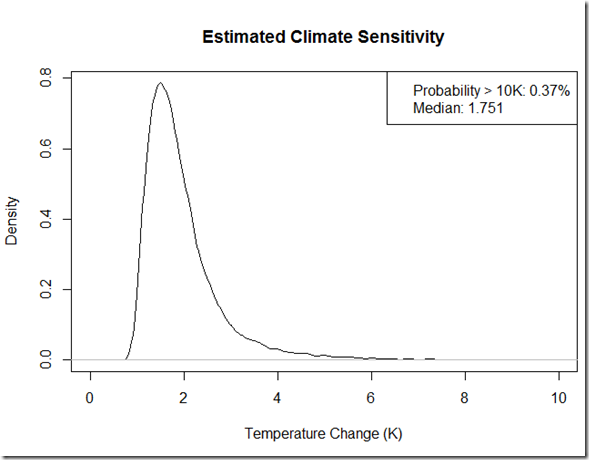
Now, for kicks, if I were to ignore the issue of λ not being a constant (and assuming it was the same for all forcings), I could flip this and get the following pdf for climate sensitivity.
As you can see, such an approach yields “most likely” estimate of around 1.8 K that is outside of IPCC likely range. However, this method in itself fails to constrain the extremely high sensitivities due to the scenarios where negative aerosols have almost completely offset GHG warming, leaving a potential of > 10 K at around 1 in 200.
Furthermore, the observant reader may have noticed that in the graphs of the two GCMs above, this method has actually overestimated the sensitivity. The GISS ER CO2 doubling forcing is 4.06 W/m^2, but the median radiative response is only -1.11 W/m^2/K, yielding a sensitivity of 3.6 K that is greater than it’s known sensitivity of 2.7 K. The median radiative response for GFDL CM2.1 using this method is merely –1.02 W/m^2/K, and with its 3.5 W/m^2 forcing this yields a sensitivity of 3.4 K that is almost its actual equilibrium sensitivity. However, the latter is likely just luck, because the GFDL CM2.1 has an extremely high uptake efficiency factor that should cause an underestimate of the sensitivity in any short-term estimate like this. One need only compare to the “effective sensitivities” in Soden and Held (2006) to see that this method underestimates the radiative response (-1.64 W/m^2/K and –1.37 W/m^2/K for GISS and GFDL respectively), and I’m not sure why exactly; my best guess at this point would have to do with the response to the high volcanic activity during this time period.
I will compare the results we get here to those of other CMIP5 models in (hopefully) my next post in order to see how effective this method might be for determining century scale sensitivity.
UPDATE (10/27):
When running my script again for the most recent post, I noticed I had used the mean of the 2004-2008 forcings rather than 2005-2011 forcings for the recent period. The change skews the PDF slightly to the left, but otherwise does not result in a huge change. The script has been updated in the link below. Here is the updated look:
Code
Please acknowledge any code or data used from this post. Thanks!
References
Forster and Gregory (2006): http://journals.ametsoc.org/doi/pdf/10.1175/jcli3611.1
Soden and Held (2006): http://www.gfdl.noaa.gov/bibliography/related_files/bjs0601.pdf
Winton et al. (2010): http://www.met.igp.gob.pe/publicaciones/2010/efficacy[1].pdf
Hansen et al. (2005): http://pubs.giss.nasa.gov/docs/2005/2005_Hansen_etal_2.pdf
Held et al. (2010): http://journals.ametsoc.org/doi/abs/10.1175/2009JCLI3466.1
Levitus et al. (2012): http://www.agu.org/pubs/crossref/pip/2012GL051106.shtml
Hansen et al. (2011) http://www.columbia.edu/~jeh1/mailings/2011/20110415_EnergyImbalancePaper.pdf







[…] interesting blog posts on climate sensitivity. Troy CA here and Paul_K at Lucia’s here. I haven’t parsed either post, but both are by thoughtful […]
Pingback by Two Blogs on Climate Sensitivity « Climate Audit — October 22, 2012 @ 10:23 am
Hi Troyca,
As well as making estimates from models, it is possible to make an estimate from empirical TOA energy balance data (poorly constrained though it is) and ARGO data. Please take a read of this and let me know what you think:
Comment by tallbloke — October 22, 2012 @ 12:07 pm
Hi Tallbloke,
Note that I am indeed making my estimate from the OHC and surface temperature observations, not models. The Levitus et al. (2012) is available from NOAA, and where ARGO data is available the NOAA OHC estimate uses it. I use GCMs for three things I can think of in the above post:
1) Showing that the difference is estimated forcing over the period primarily comes from different aerosol efficacies.
2) Verifying that using 5-yr diffs of OHC can give reasonably accurate estimates for average TOA imbalance (and determine my range for percentage of this energy taken up by the 0-2000m slab).
3) Comparing the results derived from observations to those from GCMs.
From your link, one interesting thing I thought was brought up was using recent CERES observations as a check on the instrument changes in the early part of the 21st century. This is something that presumably Loeb et al (2012): http://www.nature.com/ngeo/journal/vaop/ncurrent/full/ngeo1375.html would have looked at, though I’m not sure. Unfortunately, as I’ve discussed several times (and I’m certainly not the first), looking at TOA fluctuations over interannual variations driven by ENSO does a poor job at estimating sensitivity. Having a large external forcing, such as Pinatubo during the ERBE record can help, but you get into issues with the nonlinearity of the response that we’ve been discussing at the Blackboard recently (and is linked to in the post above). That is why using OHC, which extends much farther than the satellite record, I think provides a better estimate for sensitivity.
On the more critical parts of that post, I note first that it is only using 0-700m (understandable given the post is 2 years old), so could miss a sizeable chunk of the energy of the system. Regardless, I’m not sure how one could reconcile the rising OHC with a negative imbalance, nor do I see a numerical estimate of sensitivity in that post. Is there a specific part from that post that I am missing that is particularly relevant here? I note that the author suggests that “OHC reconstructions before 2003 are simply wrong”, but to me this is a tremendous leap to make based simply on three years of overlapping CERES and OHC during the “problem” period.
Comment by troyca — October 22, 2012 @ 1:31 pm
Hi Troy, and thanks for the detailed reply.
The Berenyi post doesn’t attempt a sensitivity calculation as you noted, I brought it to your attention for a few reasons.
Firstly, the ARGO data, until its latest set of ‘adjustments’ towards the end of 2011 did indeed show a fall from 2003-2009. Craig Loehle also plotted it and got the same result.
Secondly, my own opinion isn’t so much that “OHC reconstructions before 2003 are simply wrong”, but that there is a serious splicing issue between the XBT data and ARGO around 2003. I tried to encourage Peter Berenyi to try a few different ‘splicing factors’ to see at what value the fit optimised with the CERES data, but he didn’t find the time, which is a pity.
Thirdly, I have found that a simple model which uses a TSI proxy (sunspot number) fits the OHC data better as a forcing. To build this I first identified the value at which the ocean neither gains nor loses energy from a level period of SST in the C19th, before co2 became an issue. Then I made a cumulative running total of sunspot numbers departing from this ‘ocean equilibrium value’. Then I scaled this to the empirically observed fluctuation over the solar cycle in the 37month smoothed temperature record (around 0.08C). This curve falls from around 1880 to 1935, then rises to 2003 before topping out and falling slightly. It accounts for around 0.3C of the rise in SST over the C20th. I am making the assumption that this includes the terrestrial amplification of the solar signal outlined in Nir Shaviv’s JGR paper ‘using the oceans as a calorimeter’ http://sciencebits.com/calorimeter
Fourthly, I incorporated that curve into a simple model along with the AMO and SOI and CO2. Together they reconstruct HADsst3 quite well. The R^2 is 0.874 using monthly data since 1876. You can see the relative contributions of the constituent forcings and the reultant curve compared to the sst daaset here: http://tallbloke.files.wordpress.com/2012/10/sst-model1.png The ‘just for fun’ forward prediction has a few assumptions built in so treat it with as much amusement as you wish. 🙂
Regarding the use of 0-700m data for OHC: The 700-2000 reading are fairly sparse and uncertainty is higher. Also, if the upper 700m were cooling from 2003-2009, I doubt that huge amounts of energy were being transferred from atmosphere to deep ocean, since thermodynamics is against it. If you’ve ever tried warming the bottom of a bath by pointing a hairdryer at the surface, you’ll see why. 😉
In summary, I fear the OHC data has been skewed by the removal of the more rapidly cooling buoys from the dataset ‘because the data are surely wrong’ as Kevin T might say.
Cheers
TB.
Comment by tallbloke — October 22, 2012 @ 3:06 pm
troyca: The NODC’s OHC data from 0-2000 meters is basically a make-believe dataset. That is there are even fewer samples at depths below 700 meters than there are above and they’re pretty darned sparse above 700 meters. Here’s a gif animation that shows the sampling at 1500 meters on a quarterly basis. There’s little to no sampling at that those depths prior to the ARGO era:

While I understand why you’re going through the efforts, I can’t see what value that NODC OHC dataset has for any attribution study. The responses you’re seeing are not based on a complete sampling of the volume of water but of a very limited sampling. A more complete sampling would dampen the responses. Also, by using volcanic aerosols as your reference, doesn’t your attribution study relate to downward shortwave radiation (visible sunlight) and not downward longwave radiation associated with greenhouse gases? You can’t mix and match the two. Volcanic aerosols impact the amount of DSR entering the oceans, and DSR penetrates the oceans to depth, while DLR only impacts the top few millimeters. Last, could you be mistaking the impacts of the eruption of El Chichon and Mount Pinatubo for the responses to the 1982/83 and 1991/92 El Niños? With 5-year smoothing NINO3.4 sea surface temperature anomalies take on a whole new look:



And here’s the raw data:
And a gif comparison:
As you can see, with the 5-year smoothing, you’d never find the big El Niño events. They simply disappear.
Regards
Comment by Bob Tisdale — October 22, 2012 @ 5:41 pm
Bob,
I understand your concern regarding the Levitus et al (2012) 0-2000m dataset given the sparse sampling. However, keep in mind that they only present 5 year averages, and they present these averages with extremely large uncertainties in the early part of the record. I do not have access to the L12 paper handy, but in the abstract they note that “Our estimates are based on historical data not previously available…” I try to use a robust method that samples from the standard errors and uses various start points, so that noise in a particular 5-yr average does not greatly affect the results. Is there somewhere that you have discussed specific errors in the L12 analysis (it would be interesting to see if we can reproduce OHC models based on the limited sampling in the historical period)?
I’m not sure what you mean by “using volcanic aerosols as your reference”. I am including volcanic forcings among other forcings…anthropogenic aerosols typically have a large effect in the SW component as well. Both the SW and LW forcings impact TOA radiation, and the units of W/m^2 are comparable…although forcings may have different efficacies depending on their type and spatial distribution, I see no reason why we cannot roughly “mix and match the two.” I do not agree that “DSR penetrates the oceans to depth, while DLR only impacts the top few millimeters” provides a substantial objection to this…whether it is absorbed in the top few millimeters or to lower depths does not change the fact that turbulent mixing re-distributes this heat within the mixed layer, nor that this get diffused to even lower depths on the timescales (5 years) we are looking at here.
Moreover, that we average out the high-frequency ENSO events here is not a problem but a feature. In the event, that for example, 5-years is dominated by an El Nino phase, this will be reflected in the increase T over that period (and consequently the lower TOA flux imbalance due to the temperature response).
-Troy
Comment by troyca — October 23, 2012 @ 10:19 am
Hi again Troy,
Just to pick up a few of those points.
“anthropogenic aerosols typically have a large effect in the SW component”
This paper is well worth studying:
http://rd.springer.com/article/10.1007/s00704-012-0685-z (free download)
A century of apparent atmospheric transmission over Davos, Switzerland
D. Lachat, C. Wehrli
“whether it is absorbed in the top few millimeters or to lower depths does not change the fact that turbulent mixing re-distributes this heat within the mixed layer”
Actually, seawater is almost completely opaque to LW. It is absorbed within the first 30 microns or so. This will mean it is more involved in evaporation than heating the bulk of the ocean because the energy is concentrated into a very thin layer of molecules. Mixing is largely due to vortices which form under wave troughs a lot further down where mid frequencies of SW penetrate. The windier it gets (increasing mixing), the more evaporation dominates. Another implication is that while it is easy for SW to enter the ocean, it is hard for LW to leave from depth, due to the very short mean free path length. The ‘greenhouse effect’ is theoretically stronger in the ocean than the air. The principle constraint on the rate at which the ocean can lose energy is the air pressure which sets the rate of evaporation. That’s down to atmospheric mass and gravity, not composition.
Cheers
TB
Comment by tallbloke — October 23, 2012 @ 3:09 pm
troyca says: “I do not agree that ‘DSR penetrates the oceans to depth, while DLR only impacts the top few millimeters’ provides a substantial objection to this…whether it is absorbed in the top few millimeters or to lower depths does not change the fact that turbulent mixing re-distributes this heat within the mixed layer, nor that this get diffused to even lower depths on the timescales (5 years) we are looking at here.”
You’re assuming that DLR does something more than add to evaporation. Evaporation is how the oceans release the vast majority of their heat. Please present the evidence that DLR has some additional effect. You cannot use the NODC OHC data (0-700 meter) to do so, because then you’d have to account for the warming in tropical OHC associated with ENSO. That is, the only times the NODC’s OHC data for the tropics (24S-24N) shows any warming is in response to the 3-year La Nina events (1954/55/56/57 & 1973/74/75/76 & 1998/99/00/01 La Ninas), and during the freakish 1995/96 La Nina. During the multidecadal periods between the 3-year La Nina events, tropical OHC cools as one would expect. You’d also have to account for the very obvious impact of the change in the sea level pressure in the North Pacific, north of 20N, in the late 1980s, which reflects a change in wind patterns there. North Pacific (north of 20N) OHC cooled until the late 1980s, then warmed in a 2-year surge, creating an upward step. It’s blatantly obvious, troyca. Can’t miss it. Without that 2-year surge, North Pacific OHC would have cooled since 1955. And if you can’t use the NODC’s 0-700 meter data to prove the existence of an anthropogenic component, you certainly cannot use the data at greater depths.
Regards
Comment by Bob Tisdale — October 23, 2012 @ 4:53 pm
Bob and Tallbloke,
As I have limited time to spend on blogging and climate science (it is a hobby), I don’t have a particular interest to get sucked into a “the greenhouse effect as we know it is wrong” rabbit hole discussion. For that there are those far more qualified (and interested) than I, among them Science of Doom. Forgive me if I am attributing arguments to you that you do not hold, but at this point we are hitting on topics that are only tangentially related to the post. I have a couple more posts “in the pipeline”, so I also ask your forgiveness if I drop this line of discussion (or at least suspend it for some time) after this comment.
Nevertheless, I have read some of your stuff with interest, Bob (and as you may have seen recently, your post with RP Sr. prompted a series of posts here), so I want to dive just a bit deeper here to see if I can better grasp your position.
1) “You’re assuming that DLR does something more than add to evaporation. Evaporation is how the oceans release the vast majority of their heat. Please present the evidence that DLR has some additional effect.”
I’m not sure what you mean by “add to evaporation”? Presuming you mean that the majority of the heat from the absorbed longwave radiation at the sea surface goes into evaporation, this does not at all contradict the idea the DLR warms the ocean. The heat that would have otherwise been lost from the mixed layer by evaporation in the absence of the LW radiation instead remains, so the mixed layer is warmer than it would have been in the absence of the DLR.
But really, there is no need to even look at the surface fluxes. A reduction in the OLR at the top-of-atmosphere will result in a positive energy imbalance into the earth system…the ocean has by far the largest heat capacity in this system, so if the extra energy caused by the reduction in OLR is not going into the ocean, where is it going? Crysophere, land surface, atmosphere? (This is not rhetorical by the way, I am wondering your view on this)
2) “That is, the only times the NODC’s OHC data for the tropics (24S-24N) shows any warming is in response to the 3-year La Nina events (1954/55/56/57 & 1973/74/75/76 & 1998/99/00/01 La Ninas), and during the freakish 1995/96 La Nina. During the multidecadal periods between the 3-year La Nina events, tropical OHC cools as one would expect.”
What reason would there be for only looking at OHC data in the tropics when determining the overall energy balance? Also, why do you believe one would “expect” tropical OHC to decrease between La Nina events? Do you believe the OHC to be decreasing/increasing in the tropics during ENSO events as a result of (a) heat transfer from other parts of the earth system (atmosphere, deeper ocean layers, other regions of the ocean), or because ENSO (b) affects the TOA flux (if so, via clouds, water vapor, Planck response)?
For fairness, I’ll answer first, noting that I’m confident that La Nina results in a net increase in energy into the earth system (at TOA) due at the very least to the temperature response (lower temperature = less OLR), and the opposite is true for El Nino. However, I haven’t seen much to indicate that this imbalance persists for any significant time beyond the current ENSO state. Moreover, I think the increase in SST results from a heat transfer from lower ocean depths into the mixed layer in the tropical Pacific (but this heat transfer itself would not impact the OHC as it is simply moving heat around…the TOA flux imbalance is actually what changes the heat content).
3) “You’d also have to account for the very obvious impact of the change in the sea level pressure in the North Pacific, north of 20N, in the late 1980s, which reflects a change in wind patterns there. North Pacific (north of 20N) OHC cooled until the late 1980s, then warmed in a 2-year surge, creating an upward step. It’s blatantly obvious, troyca. Can’t miss it. Without that 2-year surge, North Pacific OHC would have cooled since 1955”
Again, I’m not sure why if we are looking at global energy balance (as I am doing in the post), you would take a specific (albeit large) region (the North Pacific) and eliminate the period responsible for it’s largest heat accumulation? Again, how did the “change in wind patterns” result in the increased OHC…did the heat transfer from another part of the earth system during these winds (in which case, your fluke increase in OHC in one region would be balanced by a fluke decrease in another region, thus not affecting the global OHC)?
I appreciate you answering these questions…I can’t speak for others, but I think it would help me in clarifying your position.
-Troy
Comment by troyca — October 23, 2012 @ 8:02 pm
“As I have limited time to spend on blogging and climate science (it is a hobby), I don’t have a particular interest to get sucked into a “the greenhouse effect as we know it is wrong” rabbit hole discussion.”
Entirely fair enough, and thanks for your efforts to quantify the sensitivity using the consensus theory.
Comment by tallbloke — October 23, 2012 @ 11:27 pm
Very nice work.
Question: was your paper on cloud feedback accepted in final form?
Comment by stevefitzpatrick — October 22, 2012 @ 7:30 pm
Yup, see http://www.earth-syst-dynam.net/3/97/2012/esd-3-97-2012.html
Comment by troyca — October 23, 2012 @ 7:03 am
Hi Troy
Excellent work – many thanks for putting in the time and making your code and data available.
A question – why did you use a triangular distribution for the indirect aerosol forcing estimate rather than a Gaussian one as for direct aerosol forcing? Just curious.
Two comments. First, I think it is probably possible to put reasonably tight constraints on total aerosol forcing from comparisons of observed and modelled temperature changes over time in different latitude bands. I’ve done extensive work using the Forest et al 2006 4 latitude, 5 decadal changes surface temperature diagnostic and find that, although there are very serious flaws in that study and its sensitivity PDF does not correctly reflect the data, its finding of a tightly constrained total aerosol forcing is robust. FWIW, its 5-95% range is about -0.7 to -0.1 W/m^2 in the 1980s; I think that may include non GHG anthropogenic forcings (Black carbon, etc) since when I think there hasn’t been very much increase according to most estimates (GISS post Nov 2011 revision forcings excepted). Andronova & Schlesinger 2001 also got fairly tight aerosol constraints, I think.
Second, are you aware how few degrees of freedom there are in the deep ocean pentadal heat content series? Using the 0-3000m global OHC data in Levitus 2005, I estimated only about 5 DoF in 40 overlapping pentadal estimates: their AR(1) autocorrelation is 0.9. Also, using weighted LS regression on that data gives a 15-20% lower linear trend estimate than the OLS trend that Levitus gives. Further, I am dubious about all the adjustments made to the OHC data, at least pre-Argo. I have it on good authority that Levitus felt under pressure to up his trend estimates to better match GCM estimates when preparing the Levitus 2000 dataset; he actually published a data table with “arithmetic errors” in it that overstated the trend by about 20%, and apparently refused to correct the errors when told of them.
Comment by Nic L — October 25, 2012 @ 2:00 pm
Hi Nic,
Thanks for the feedback!
For the indirect aerosol forcing I used a triangular distribution because the range given by the IPCC is asymetric, unlike the direct aerosol forcing. I recall you having a post a while back at Climate Etc. about the Forest et al. (2006) paper…after your work on that, do you anticipate getting a paper out of it? Anyhow, I agree that the aerosol forcing is probably better constrained (and lower in magnitude) than the IPCC estimate I use here, if only based on the fact that the NH warming rate has been much larger than the SH rate: https://troyca.wordpress.com/2012/05/08/northern-and-southern-hemisphere-warming-in-models-and-gistemp/
Similarly, I can’t vouch for the Levitus et al. (2012) values as I have not taken an in-depth look at the paper. The only thing I will note is that I’m using the *difference* in TOA imbalance here. So, for instance, while the 1968-1979 trend might be large and increase the overall trend in OHC, in my method this actually results in a lower estimate for sensivity, because the TOA imbalance would have dropped between then and now despite an increase in forcing, which implies a larger radiative response for the temperature increase. The method is thus insensitive to a *uniform* (across time) artificial inflation in the OHC trend…you would only get an overestimate for sensitivity in the event that the most recent period (2005 – 2011) showed an inflated trend while the former period remained untouched.
Comment by troyca — October 25, 2012 @ 3:36 pm
Hi Troy
Thanks for the clarification. I had forgotten how asymmetrical the IPCC indirect aerosol forcing estimated PDF was.
I have a paper reworking the Forest 2006 study undergoing peer review. It is mainly about improving the statistical methodology.
Noted re only the change in rate OHC change mattering. It is very strange that NOAA 2005-11 figures show a large trend for 0-2000m but almost no trend for 0-700m, which is much better measured. http://www.nodc.noaa.gov/OC5/3M_HEAT_CONTENT/ I’m not sure that I believe the 0-2000m figures. My (limited) understanding of ocean processes is that it is not very easy for heat to penetrate below 700m, as upwelling counteracts the slowing diffusion by that depth. No doubt there are other processes involved – isopycnal transport, etc. Even so, I find it pretty hard to understand such a strong flow out of the bottom of the 0-700m layer with no change in its mean temperature.
BTW, have you tried using the pre-Nov11 GISS aerosol forcings, which were much lower? I suspect they were upped following Hansen’s 2011 paper arguing tht GCMs had too high ocean heat uptake and therefore must have too low aerosol forcings (as otherwise his preferred 3K climate sensitivity would give too high a 20th century temperature rise).
Comment by Nic L — October 26, 2012 @ 5:54 am
Hi Nic,
I have not tried with the old GISS aerosol forcings…in fact I was not aware until a few days ago (since Paul_K was discussing it) that they were changed on the website (I thought the update referred to simply including new data). I think Paul mentioned that they switched from using Fa to Fe? Anyhow, do you know where I can get the old forcings? Also, I’m glad to hear you’re wrote up the study with regards to Forest 2006…I would be interested in using whatever you get for the better constrained aerosol forcing change over the period I’m looking at here (~1950 – 2011) in this analysis as well.
I am also a bit curious about why there was such a large discrepancy in the 0-700m vs. 0-2000 m trend over a pretty substantial period, but as I said I have not done much investigation into this topic.
Comment by troyca — October 27, 2012 @ 9:22 am
Hi Troy
I’m emailing you the old GISS forcing data. Can you clarify what Fa and Fe refer to – I’m not familiar with these abbreviations.
I’m afraid the Forest 2006 estimate is only for the change in total aerosol forcing up to the 1980’s, from the mid-19th century if I recall correctly.
Comment by Nic L — October 27, 2012 @ 11:41 am
Thanks for the data, Nic. I realized that these different values for the aerosol forcings don’t really affect the estimate here, as I already scaled the GISS aerosol forcings to match the IPCC estimates. Anyhow, Fa and Fe are described in the “Efficacy of climate forcings” (Hansen et al 2005) paper, where Fa refers to the “adjusted forcing”, which is the TOA flux change to a forcing if the climate is held fixed but the stratosphere is allowed to adjust, and Fe refers to the “effective forcing” that is I believe the “efficacy” of the forcing (determined from a long-term response) multiplied by Fs (the TOA flux change if only SST is held fixed when the forcing is introduce but other components are allowed to adjust).
Anyhow, I haven’t read the Forest 2006 paper…is it possible to apply their methodlogy to produce estimates for more recent aerosol forcings?
Comment by troyca — October 27, 2012 @ 6:04 pm
[…] post forms part 2 of the series I started in the last post, which focused on using the energy balance over the period of 0-2000m OHC data to estimate […]
Pingback by CMIP5 Effective Sensitivity vs. Radiative Response in Last 40 Years « Troy's Scratchpad — October 27, 2012 @ 2:17 pm
Using this post as a can opener into my review of the sensitivity work, I’ve had to resort to your code in an attempt to disambiguate the description above, and I’m only barely into it, having only reached this line in the first file:
GFDL.OHC.anom<-window(ts(read.table("GFDL-CM2_1/GFDL-CM2_1_OHC_r1_1951-2015.txt")[[2]], start=1951), start=1955)
But I think that line should have been
GFDL.OHC.anom<-window(ts(read.table(paste(url,"GFDL-CM2_1/GFDL-CM2_1_OHC_r1_1951-2015.txt",sep=''))[[2]], start=1951), start=1955)
For us tyros, what does GFDL stand for?
Comment by Joe Born — October 28, 2012 @ 2:58 am
Thanks Joe, you are correct about the GFDL line, and it’s correction (when I convert the script from using my local working directory to my public archive I sometimes miss these errors). I have updated the script to reflect this. “GFDL” stands for “Geophysical Fluid Dynamics Laboratory”, in this case it is short-hand for the GFDL climate model version 2.1. Coincidentally, I was not familiar with the word “tyros” before, so thanks for introducing me to that!
Comment by troyca — October 28, 2012 @ 1:34 pm
[…] this half-baked post, I want to look a bit more at the issue of how the radiative response (λ) in our familiar equation (ΔN = ΔF + λ*ΔT) changes as we progress through the 1% CO2 increase per year to doubling […]
Pingback by Changes in feedback strength with time: a look at the 1pct2xCO2 GFDL CM2.1 experiment « Troy's Scratchpad — November 7, 2012 @ 7:17 pm
[…] from an examination of the radiation budget when Pinatubo erupted in 1991: a value of 1.4°K, the other comes from an evaluation of the global temperatures and the heat content of the upper 2000 m of […]
Pingback by Troposhsphere And Sea Surface Temperature: 18 Years With No Trend! Natural Factors Dominate — November 9, 2012 @ 10:25 am
[…] the sensitivity estimate is straight-forward and should be seriously considered (I’ve used a similar approach and got similar results). Nic Lewis goes into more detail here. It is his rework of the […]
Pingback by Climate Sensitivity, the Wall Street Journal, and Media Matters « Troy's Scratchpad — December 22, 2012 @ 10:58 am
[…] Estimating Sensitivity from 0-2000m OHC and Surface Temperatures […]
Pingback by ¿Se esconde el calentamiento global en el fondo del mar? « PlazaMoyua.com — January 20, 2013 @ 6:09 am
I blog quite often and I really thank you for your content.
The article has really peaked my interest. I’m going to book
mark your website and keep checking for new details about once per week.
I opted in for your RSS feed as well.
Comment by window — November 27, 2018 @ 2:30 am