Initial thoughts on the Schmidt et al. commentary in Nature

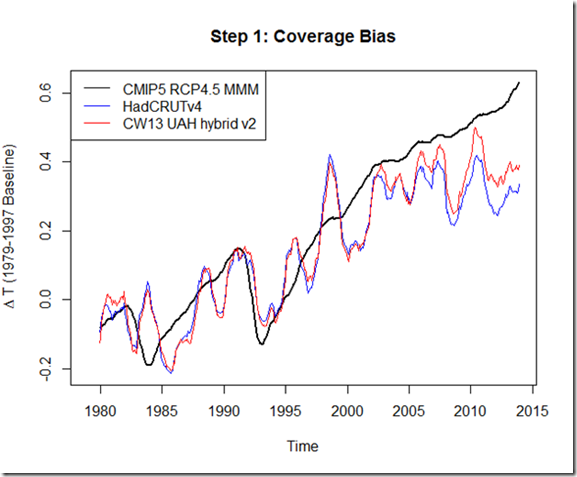
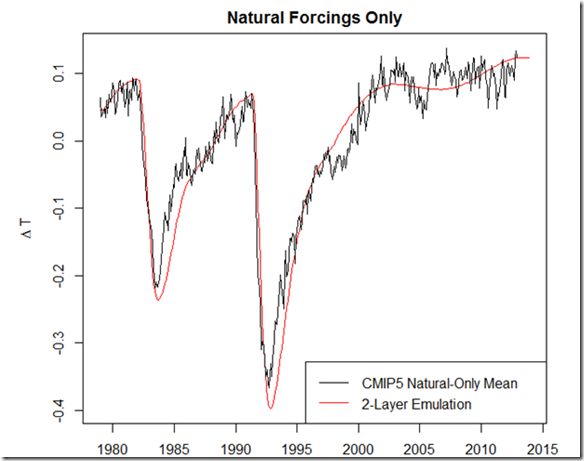
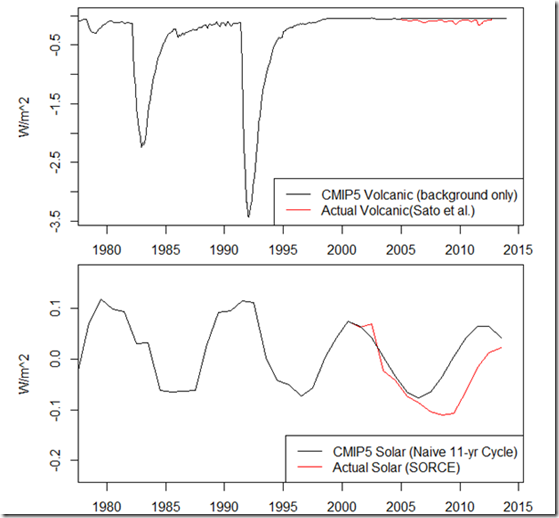
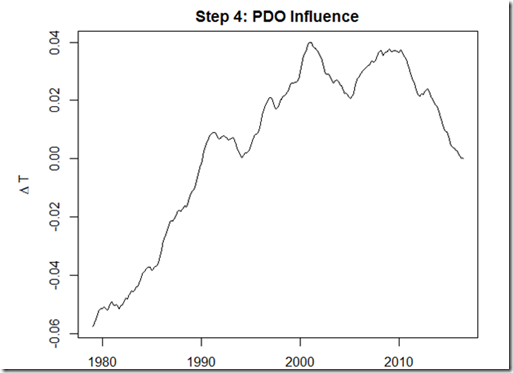
Thanks to commenter Gpiton, who on my last post about attributing the pause, alerted me to the commentary by Schmidt et al (2014) in Nature (hereafter SST14).  In the commentary, the authors attempt to see how the properties of the CMIP5 ensemble and mean might change if updated forcings were used (by running a simpler model), and find that the results are closer to the observed temperatures (thus primarily attributing the temperature trend discrepancy to incorrect forcings).  Overall, I don’t think there is anything wrong with the general approach, as I did something very similar in my last post.  However, I do think that some of the assumptions about the cooler forcings in the "correction" are more favorable to the models than others might choose, and a conclusion could easily be misinterpreted.  This is my list of comments that, were I a reviewer, I would submit:

Comment #1: The sentence

We see no indication, however, that transient climate response is systematically overestimated in the CMIP5 climate models as has been speculated, or that decadal variability across the ensemble of models is systematically underestimated, although at least some individual models probably fall short in this respect.

is vague enough to perhaps be technically true while at the same time giving the (incorrect, IMO) impression they have found that models are correctly simulating TCR or decadal variability.  It may be technically true in that they find "no indication" of bias in TCR or internal variability, due to the residual “prediction uncertainty”, but this is one of those "absence of evidence is not evidence of absence" scenarios, where even if the models WERE biased high in their TCR there would be no indication by this definition.  By the description in the commentary,  the adjustments only remove about 60-65% of the discrepancy.  The rest of the discrepancy may be related to non-ENSO noise, but it also may be related to TCR bias, and would be what we expect to see if , for example, the "true" TCR was 1.3K (as in Otto et al., 2013) vs. the CMIP5 mean of 1.8K.  Obviously, the reference to Otto et al., (2013) might be mistaken by some to suggest an answer/refutation to that study (which used a longer period to diagnose TCR in order to reduce the "noise"), but clearly this would be wrong.  Had I been a reviewer, I would have suggested changing the wording: "The residual discrepancy may be consistent with an overestimate of the transient climate response in CMIP5 models [Otto et al., 2013] or an underestimate of decadal variability, but it is also consistent with internal noise unrelated to ENSO, and we thus cannot neither rule out nor confirm any of the explanations in this analysis."  Certainly has a different feel, but it essentially communicates the same information, and is much less likely to be misinterpreted by the reader.

Comment #2: Regarding the overall picture of updated forcings, it is worth pointing out that IPCC AR5 Chapter 9  [Box 9.2, p 770] describes a largely different opinion (ERF = ”effective radiative forcing”)

For the periods 1984–1998 and 1951–2011, the CMIP5 ensemble-mean ERF trend deviates from the AR5 best-estimate ERF trend
by only 0.01 W m–2 per decade (Box 9.2 Figure 1e, f). After 1998, however, some contributions to a decreasing ERF trend are missing
in the CMIP5 models, such as the increasing stratospheric aerosol loading after 2000 and the unusually low solar minimum in 2009.
Nonetheless, over 1998–2011 the CMIP5 ensemble-mean ERF trend is lower than the AR5 best-estimate ERF trend by 0.03 W m–2 per
decade (Box 9.2 Figure 1d). Furthermore, global mean AOD in the CMIP5 models shows little trend over 1998–2012, similar to the
observations (Figure 9.29). Although the forcing uncertainties are substantial, there are no apparent incorrect or missing global mean
forcings in the CMIP5 models over the last 15 years that could explain the model–observations difference during the warming hiatus.

(My emphasis).  Essentially, the authors of this chapter find a discrepancy of 1.5 * 0.03 = 0.045 W/m^2 over the hiatus, whereas SST14 use a discrepancy of around 0.3 W/m^2, which is nearly 7 times larger!  And there does not appear to have been new revelations about these forcings since the contributions to the report were locked down – the report references the "increasing stratospheric aerosol loading after 2000" and "unusually low solar minimum in 2009" mentioned in the  commentary.  Regarding the anthropogenic aerosols, both the Shindell et al, (2013) and  Bellouin et al., (2011) papers referenced by SST14 for the nitrate and indirect aerosol estimates are also referenced in that AR5 chapter, and Shindell was a contributing author to the chapter.  This is not to say that the IPCC is necessarily right in this matter, but it does suggest that not everyone agrees with the magnitude of the forcing difference used in SST14.

Comment #3:  Regarding the solar forcing update, per box 1, SST14 note: "We multiplied the difference in total solar irradiance forcing by an estimated factor of 2, based on a preliminary analysis of solar-only transient simulations, to account for the increased response over a basic energy balance calculation when whole-atmosphere chemistry mechanisms are included."

I would certainly want to see more justification for doubling the solar forcing discrepancy (this choice alone accounts for about 15% of the 1998-2012 forcing discrepancy used)!  If I understand correctly, they are saying that they found that the transient response to the solar forcing is approximately double the response to other forcings in their preliminary analysis.  But this higher sensitivity to a solar forcing would seem to be an interesting result in its own right, and I would want to know more about this analysis, and what simulations were used – was this observed in one, some, most, or all of the CMIP5 models?  After all, if adjusting the CMIP5 model *mean*, it would be important to know that this was a general property shared across most of the CMIP5 models.

Comment #4: For anthropogenic tropospheric aerosols, two adjustments are made.  One for the nitrate aerosol forcing, and the second for the aerosol indirect effect.  SST14 notes that only two models include the nitrate aerosol forcing, whereas half contain the aerosol indirect effect, and so the ensemble and mean are adjusted for these.  But it is not clear to me if the individual runs for each of the CMIP5 models are adjusted (and thereby no adjustments are made to runs from models that include the effect), and the mean recalculated, or if simply the mean is adjusted.  The line "…if the ensemble mean were adjusted using results from a simple impulse-response model with our updated information on external drivers" makes me think the latter.  But if it is this latter case, clearly this is incorrect – if half of the models already include the effect, you would be overcorrecting by a factor of 2 if you adjusted the mean by this full amount (perhaps the -0.06 is halved before the adjustment is actually made, but it is not specified).

Comment #5: Regarding the indirect aerosol forcing, Belloin et al., (2011) is used as the reference, which uses the HadGEM2-ES model.  It is worth noting the caveats:

The first indirect forcing in HadGEM2‐ES, which can be diagnosed to the first order as the difference between total and direct forcing [Jones et al., 2001] might
overestimate that effect by considering aerosols as externally mixed, whereas aerosols are internally mixed to some extent.  By comparing with satellite retrievals, Quaas et al. [2009] suggest that HadGEM2 is among the climate models that overestimate the increase in cloud droplet number concentration  with aerosol optical depth and would therefore simulate too strong a first indirect effect.

Moreover, I am not quite sure the origin of the -0.06 W/m^2.  Belloin et al., (2011) suggest an indirect effect from nitrates that is ~40% the strength of the direct effect.  So if only nitrate aerosols increased over the post-2000 period, I would expect an indirect effect of ~ -0.01 W/m^2.  It seems to me that this must include the much-larger effect of sulfate aerosols, which leads me to my next comment…

Comment #6: Sulfate Aerosols.  Currently, sulfate aerosols constitute a much larger portion of the aerosol forcing than do other species (nitrates in particular).  I presume that for #5, the indirect aerosol forcing of that magnitude would need to result from an increase in sulfur dioxide emissions.  But as per the reference of Klimont et al., (2013) in my last post, global sulfur dioxide emissions have been on the decline since 1990, and since 2005 (when the CMIP5 RCP forcings start) the Chinese emissions have been on the decline as well (only India continues to increase).  Rather than the lack of indirect forcing artificially warming the models relative to observations, it seems like it has been creating a *cooling* bias over this period, if you use the simple relationship between emissions and forcing as in Smith and Bond (2014).  In fact, since 2005 (according to Klimont et al., 2013 again), sulfur dioxide emissions have declined faster than in 3 of the 4 RCP scenarios.  It seems likely to me that the decline in sulfur dioxide emissions over this period (and it’s corresponding indirect effect) would more than counteract the tiny bias from the NO2 emissions. 

Conclusion:

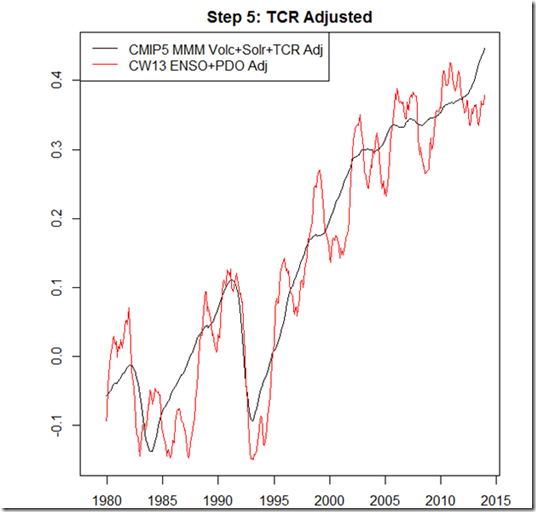
Having just done a similar analysis, I thought it important to put the Schmidt et al. (2014) Nature commentary in context.  There is enough uncertainty around the actual forcing progression during the "hiatus" to find a set of values that attribute most of the CMIP5 modeled / observed temperatures to forcing differences.  However, the values chosen by SST14 do seem to represent the high end of this forcing discrepancy, and it appears that most of authors of AR5 chapter 9 believe the forcing discrepancy to be much more muted.  Moreover, the SST14 commentary should not be taken to be a response to longer period, more direct estimates of TCR, such as that of Otto et al., (2013).  Specifically, the TCR bias found in that study would be perfectly consistent with the remaining discrepancy and uncertainty present between the CMIP5 models and observations.    

Breaking down the discrepancy between modeled and observed temperatures during the “hiatus”

 

Introduction

There are many factors that have been proposed to explain the discrepancy between observed surface air temperatures and model projections during the hiatus/pause/slowdown. One slightly humorous result is that many of the explanations used by the “Anything but CO2” (ABC) group – which argues that previous warming is caused by anything (such as solar activity, the PDO, or errors in observed temperatures) besides CO2 – are now used by the “Anything but Sensitivity” (ABS) group, which seems to argue that the difference between modeled and actual temperatures may be due to anything besides oversensitivity in CMIP5 models. And while many of these explanations likely have merit, I have not yet seen somebody try to quantify all of the various contributions together. In this post I attempt (perhaps too ambitiously) to quantify likely contributions from coverage bias in observed temperatures, El Nino Southern Oscillation (ENSO), post-2005 forcing discrepancies (volcanic, solar, anthropogenic aerosols and CO2), the Pacific Decadal Oscillation (PDO), and finally the implications for transient climate sensitivity.

Since the start of the “hiatus” is not well defined, I will consider 4 different start years, all ending in 2013. 1998 is often used because of the large El Nino that year, which minimizes the magnitude of the trend starting in that year.  On the other hand, the start of the 21^st century is sometimes considered as well. Moreover, I will use HadCRUTv4 as the temperature record (since this is the more cited to represent the hiatus), which will show a larger discrepancy at the beginning than GISS, but will also show a larger influence from the coverage bias. The general approach here is to consider that IF the CMIP5 multi-model mean (for RCP4.5) is unbiased, what percentage of the discrepancy can we attribute to the various factors? Only at the end do we look into how the model sensitivity may need to be “adjusted”. Note that each of the steps below are cumulative, building off of previous adjustments. Given that, here is the discrepancy we start with:

Start year	HadCRUT4 (K/Century)	RCP4.5 MMM (K/Century)
1998	0.44	2.27
1999	0.75	2.16
2000	0.44	2.01
2001	-0.08	1.92

 

Code and Data

My script and data for this post can all be downloaded in the zip package here. Regarding the source of all data:

· Source of “raw” temperature data is HadCRUTv4

· Coverage-bias adjusted temperature data is from Cowtan and Way (2013) hybrid with UAH

· CMIP5 multi-model mean for RCP4.5 comes from Climate Explorer

· Multivariate ENSO index (MEI) comes from NOAA by way of Climate Explorer

· Total Solar Irradiance (TSI) reconstruction comes from SORCE

· Stratospheric Aerosol Optical Thickness comes from Sato et al., (1993) by way of GISS

· CMIP5 multi-model mean for natural only comes from my previous survey

· PDO index comes from the JISAO at the University of Washington by way of Climate Explorer.

 

Step 1: Coverage Bias

For the first step, we represent the contribution from coverage bias using the results from Cowtan and Way (2013). This is one of two options, with the other being to mask the output from models and compare it to HadCRUT4. The drawback of using CW13 is that we are potentially introducing spurious warming by extrapolating temperatures over the Arctic. The drawback of masking, however, is that if indeed the Arctic is warming faster in reality than it is in the multi-model-mean, then we are missing that contribution. Ultimately, I chose to use CW13 in this post because it is a bit easier, and because it likely represents an upper bound on the “coverage bias” contribution. I may examine the implications of using masked output in a future post.

The above graph is baselined over 1979-1997 (prior to the start of the hiatus), which highlights the discrepancy that occurs during the hiatus.

Start year	S1: HadCRUT4 Coverage Adj (CW13, K/Century)	RCP4.5 MMM (K/Century)
1998	1.10	2.27
1999	1.38	2.16
2000	1.05	2.01
2001	0.54	1.92

Step 2: ENSO Adjustment

The ENSO adjustment here is simply done using multiple linear regressions, similar to Lean and Rind (2008) or Foster and Rahmstorf (2011), except using the exponential decay fit for other forcings, as described here.  While I have noted several problems with the LR08 and FR11 approach with respect to solar and volcanic attribution, which I mention in the next step, I also found that ENSO variations are high enough frequency so as to be generally unaffected by other limitations in the structural fit of the regression model.

 

Step 3: Volcanic and Solar Forcing Updates for Multi-Model-Mean

The next step in this process is a bit more challenging. We want to see to what degree updated solar and volcanic forcings would have decreased the multi-model mean trend over the hiatus period, but it is quite a task to have all the groups re-run their CMIP5 models with these updated forcings. Moreover, as I mentioned above and in previous posts (and my discussion paper), simply using linear regressions does not adequately capture the influence of solar and volcanic forcings. Instead, here I use a two-layer model (from Geoffrey et al., 2013) to serve as an emulator for the multi-model mean, fitting it to the mean of those natural-only forcing runs over the period. This is a sample of the “best fit”, which seems to adequately capture the fast response at least, even if it may be unable to capture the response over longer periods (but we only care about the updates from 2005-2013):

 

And here are the updates to the solar and volcanic forcings (updates in red). For the volcanic forcing, we have CMIP5 volcanic aerosols returning to background levels after 2005. For the solar forcing, we have CMIP5 using a naïve, recurring 11-year solar cycle, as shown here, after 2005.

The multi-model mean is then “adjusted” by the difference between our emulated volcanic and solar temperatures from the CMIP5 forcings and the observed forcings. The result is seen below:

Over the hiatus period, the effect of the updated solar and volcanic forcings reduces the multi-model mean trend by between 13% and 20%, depending on the start year.

 

Updated anthropogenic forcings?

With regards to the question of how updated greenhouse gas and aerosols forcings may have contributed to the discrepancy over the hiatus period, it is not easy to get an exact number, but based on evidence of concentrations and emissions that I’ve seen, there does not seem to be a significant deviation between the RCP4.5 scenario from 2005-2013 and what we’ve observed. This is unsurprising, as the projected trajectories for all of the RCP scenarios (2.6, 4.5, 6.0, 8.5) don’t substantially deviate until after this period.

For instance, the RCP4.5 scenario assumes the CO2 concentration goes from 376.8 ppm in 2004 to 395.6 ppm in 2013. Meanwhile, the measured annual CO2 concentration has gone from 377.5 ppm in 2004 to 396.5 ppm in 2013. By my back-of-the-envelopment calculation, this means we have actually experienced an increase in forcing of 0.002 W/m^2 more than in the RCP4.5 scenario, which is a magnitude away from being relevant here.

For aerosols, Murphy (2013) suggests little change in forcing from 2000-2012, the bulk of the hiatus period examined. Klimont et al (2013) find a reduction in global (and Chinese) sulfur dioxide emissions since 2005, compared to the steady emission used in RCP4.5 from 2005-2013, meaning that updating this forcing would actually increase the discrepancy between the MMM and observed temperatures. However, it seems safer to simply assume that mismatches between projected and actual greenhouse gas and aerosol emissions have contributed a likely maximum of 0% to the observed discrepancy over the hiatus, and it is quite possible that they have contributed a negative amount (that is, using the observed forcing would increase the discrepancy).

 

Step 4 & 5: PDO Influence and TCR Adjustment

Trying to tease out the “natural variability” influence on the hiatus is quite challenging. However, most work seems to point to the variability in the Pacific: Trenberth and Fasullo (2013) suggest the switch to the negative phase of the PDO is responsible, causing changing surface wind patterns and sequestering more heat in the deep ocean. Matthew England presents a similar argument, tying in his recent study to that of Kosaka and Xie (2013) over at Real Climate.

In general, the idea is that the phase of the PDO affects the rate of surface warming. If we assume that the PDO index properly captures the state of the PDO, and that the rate of warming is proportional to the PDO index (after some lag), we should be able to integrate the PDO index to capture the form of the influence on global temperatures. Unfortunately, because of the low frequency of this oscillation, significant aliasing may occur between the PDO and anthropogenic component if we regress this form directly against observed temperatures.

There are thus two approaches I took here. First, we can regress the remaining difference between the MMM adjusted for updated forcings and the ENSO-adjusted CW13, which should indicate how much of this residual discrepancy can be explained by the PDO. In this test, the result of the regression was insignificant – the coefficient was in the “wrong” direction (implying that the negative phase produced warming), and R^2=0.04. This is because, as Trenberth et al. (2013) note, the positive phase was in full force from 1975-1998, contributing to surface warming. But the MMM matches too well the rate of observed surface warming from 1979-1998, leaving no room for the natural contribution from the PDO.

To me, it seems that if you are going to leave room for the PDO to explain a portion of the recent hiatus, it means that models probably overestimated the anthropogenic component of the warming during that previous positive phase of the PDO. Thus, for my second approach, I again use the ENSO-adjusted CW13 as my dependent variable in the regression, but in addition to using the integrated PDOI as one explanatory variable, I include the adjusted MMM temperatures as a second variable. This will thus find the best “scaling” of the MMM temperature along with the coefficient for the PDO.

After using this method, we indeed find the “correct” direction for the influence of the PDO:

According to this regression, the warm phase of the PDO contributed about 0.1 K to the warming from 1979-2000, or about 1/3 of the warming over that period. Since shifting to the cool phase at the turn of the 21^st century, it has contributed about 0.04 K cooling to the “hiatus”. This suggests a somewhat smaller influence than England et al. (2014) finds.

For the MMM coefficient, we get a value of 0.73. This would imply that the transient climate sensitivity is biased 37% too high in the multi-model mean. Since the average transient climate sensitivity for CMIP5 is 1.8 K, this coefficient suggests that the TCR should be “adjusted” to 1.3 K. This value corresponds to those found in other observationally-based estimates, most notably Otto et al. (2013).

When we put everything together, and perform the “TCR Adjustment” to the CMIP5 multi-model-mean as well, we get the following result:

 

Conclusion

Using the above methodology, the table below shows the estimated contribution by each factor to the modeled vs. observational temperature discrepancy during the hiatus (note that these rows don’t necessarily add up to 100% since the end result is not a perfect match):

Start Year	Step1: Coverage Bias	Step2: ENSO	Step3: Volc+Solar Forcings	Step4: PDO (surface winds & ocean uptake)	Step5: TCR Bias
1998	36%	10%	17%	2%	28%
1999	45%	0%	23%	6%	35%
2000	39%	9%	23%	7%	28%
2001	31%	16%	20%	5%	21%

According to this method, the coverage bias is responsible for the greatest discrepancy over this period. This is likely contingent upon using Cowtan and Way (2013) rather than simply masking the CMIP5 MMM output (and using HadCRUT4 rather than GISS). Moreover, 65% – 79% of the temperature discrepancy between models and observations during the hiatus may be attributed to something other than a bias in model sensitivity. Nonetheless, this residual warm bias in the multi-model mean does seem to exist, such that the new best estimate for TCR should be closer to 1.3K.

Obviously, there are a number of uncertainties regarding this analysis, and many of these uncertainties may be compounded at each step. Regardless, it seems pretty clear that while the hiatus does not mean that surface warming from greenhouse gases has ceased – given the other factors that may be counteracting such warming in the observed surface temperatures – there is still likely some warm bias in the CMIP5 modeled TCR contributing to the discrepancy.