A New Model for UHI in US 1970-2000 Temperature Trends

Background

Since starting this blog, I’ve been trying to determine the UHI effect based on how changing populations trends correlate with changing temperature trends at various stations.  I believe the most successful demonstration of that was here.

Along that path, I stumbled upon the NHGIS, which gives  access to aggregate census data. Over the past few weeks I’ve been working with this data to determine any variables that might serve as better proxies for this “UHI” effect.

The Data

All intermediate data, code, and my downloaded NHGIS datasets can be retrieved from here (the biggest package yet).

The temperature data, once again, is USHCNv2.

The data for my variables (e.g. Num Vehicles Availables, Aggregate Family Income, etc.) is from NHGIS.  The availability of differents topics can be seen here, and based on the limitation of the data and what I thought could possibly be proxies for land use/UHI, I was left with only a few choices.  Notes on how I got from the raw NHGIS datasets to the variables can be seen in the Origins.txt included in the package above.

Ultimately, I found that many of these variables were decent proxies for the UHI effect, but few were independent of each other and most of them did not perform better than population.

However, the Aggregate Family Income of a “place” DOES seem to be a better proxy for UHI than population, which is unsurprising given that economic development typically spurs the surface and land-use changes.  Furthermore, the number of workers in Agriculture, Fishing, Forestry, and Hunting seems to be pretty orthogonal to Aggregate Family Income, and also a decent proxy for UHI in its own right.  It is negatively correlated, which also makes sense, because a decrease in these sorts of jobs suggests an “urbanization”.  Regressions using these these two explanatory variables has led to the best results.

One note on Aggregate Family Income: For determining the magnitude of the effect, I use an inflation-adjusted value for each year, calculated using this site.  The inflation-adjusted value is reported in 1970’s dollars.  While inflation does not affect the correlation, it can greatly affect the estimated magnitude of UHI based on our model.

The Method (#1)

The first method I use is very similar to the one I used with population previously, but I will reproduce some of the basic points here.

1) For each station, the linear temperature trend (dT) is calculated based on the data from 1970-2000.  A station is only included if it reports an annual temperature for at least 7 years in every decade from 1970-2000.

2) Similarly, a trend is calculated for both Income and AgrWork (and other variables) at each station, using the 1970, 1980, 1990, and 2000.  The trend is in terms of the log of these variables, so dI and dA (which I will use for short-hand) refer to the log-difference each year.

3) Based on latitude and longitude, we match all close station pairs.  A match is determined based on approximate distance in km between the station pairs.  If the difference between two stations is less than the “threshold” distance, the pair is included.

4) We then regress the difference between two temperature trends of nearby stations against the difference in log trends of Income and AgrWorkers in those same stations.  So we try to find an equation of the form (TempTrend2 – TempTrend1) = a * (logIncomeTrend2-logIncomeTrend1) + b * (logAgrWorkersTrend2 – logAgrWorkersTrend1) + c

The Method (#2)

The other method I used was to simply compare all stations at once.  Steps 1) and 2) are exactly the same as above.  Then,

3) The U.S. is broken up into 2.5 x 2.5 degree grid cells, and the average temperature trend is calculated for each grid cell.  A value for dtAdj at each station is determined, which is the temperature trend for a particular station MINUS the average temperature trend of all other station temperature trends in its own grid cell.

4)  The dtAdj for each station is then compared against the resulting dI and dA for that station.

Step #3, is used to remove the spatial auto-correlation that I’ve encountered before, since we adjust each station’s temperature trend by others in the region.

Why have this second method at all?  First of all, it allows for comparing all stations at once, rather than over-representing those stations that have more stations clustered nearby.  Second, it allows for us to use stations that are more solitary, taking advantage of nearby ones that may have valid temperature data but do not have data for the other variables.  In other words, while we are limited to some 400 stations of those that have our Income data  AND temperature data, we can use all 800 or so that have at least temperature data to perform our regional adjustments.

Of course, in the event that we do encounter spatial auto-correlation and the Income increases more in certain grid-cells than others, we are almost certain to get an underestimate of the slope, since we’re subtracting the average trend even if the UHI effect be a net positive.

Results

This first table shows the results of running Method #2 on the Raw, F52, and TOB USHCN datasets, regressing dtAdj against dI and dA. 

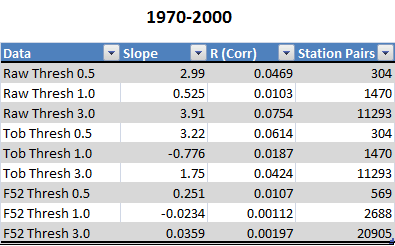
This second table shows the results of method #2, where we perform the pairwise comparisons.  I’ve shown the results at various threshold distances for what constitutes a match.

In both methods, there seems to be a fairly robust signal (outside of the F52 dataset).  I will continue forward using the TOB set, with more explanation of why in the discussion at the end.

Magnitude of the Effect

At this point, it’s worthwhile to take a look at the magnitude of the effect.  Though there are more sophisticated methods for calculating the yearly US anomaly out there, I only needed an approximation here, and so the method I used was fairly simple: use a 5×5 degree grid for the US, calculate the average anomaly for each grid cell, then average the grid cells.

Here’s a graph that shows my resulting anomalies versus that of GISS. (Note that they have different baselines).

They match up pretty well, with the trends fairly close.

Now, in order to calculate the magnitude of the effect, I simply subtract the (coefficient for each variable times the number of years that have elapsed times the annual trend of that variable at that station)  from the anomaly for the station.

Clearly, this is going to be extremely sensitive to both the coefficient AND the annual trend of the variable at a particular station.  For something like population, the annual trend is pretty straightforward if we have the data.  However, with Income it was necessary to adjust for inflation, since an increase in Aggregate Income that is only par with inflation does not suggest economic development.

Regarding the coefficients, I will show the adjustments using the higher-end ( 9.33, -2.046) and lower-end (3.22, -1.4) of our results from above:

On the higher end, we see about 25.4% of our trend due to UHI during this time period, and on the lower end we have about 9.4%.

Discussion

We’re left with a range likely in between 10% and 25% for the U.S. during this time period using the TOB dataset.  As I’ve discussed before, it is not surprising that we find a weak to non-existent signal in the F52 adjusted data-set.  While it is possible that this is due to perfectly removing the UHI effect, it is also quite likely that the infilling of data has only added noise to dilute the signal.  Furthermore, when the temperature readings have been adjusted to match nearby stations, we can hardly expect our pairwise tests to then yield anything meaningful.  

To me, the real wildcards here are the inhomogeneity adjustments. On the one hand, we may be getting a correlation here between the the instrument-related adjustments and the economic development near a particular station, in which case we are overestimating the effect of UHI.  On the other hand, it may be that adjusting for station equipment type and location moves (and avoiding the pairwise temperature trend adjustments) may in fact increase the signal, suggesting that what we have is an underestimate.  This is likely to be my next avenue of research, when I get a chance.

Mid-month report on my UAH Nov Anomaly Bet

For a bit of fun, and now that Nov 15th has reported its daily anomaly at the AMSU website, I’d thought I’d look over the chances of my “system” being right.  (Keep in mind it’s really a system for the average Aqua Ch5 daily anomalies for the month, not necessarily what UAH reports).   This system simply takes the daily anomalies for SST from 112 days earlier and multiplies them by 1.57 to try and get the Aqua daily anomalies.

State of the Prediction: Unlikely.

My bet was on .118 C for the monthly anomaly.  The average of the daily anomalies for Nov 1 – Nov 15 so far is  .301 C*.  This means that the remaining 15 days must average (-0.065 C) for me to win.  That is, the end of November must spend a good deal of time in negative territory.   

*Note: Nov 11, 12, & 13 are all missing, so I estimated their values based on a straight line between the two closest days.  So since Nov 10 = 252.68 K and Nov 14 = 252.424 K, the values I estimated are 252.616, 252.552, and 252.488.

Updated Graphs of Aqua vs. offset SST

Some Hope?

Two things might save my guess here:  1) The temperature has been rapidly dropping over the past 8 days.  As of Nov 15th, the daily anomaly was only 0.153 C (still a ways above what I need it to be).   And 2) the baseline temperature flattens out in the 2nd half of Nov. 

The average temperature drop over the past 8 days is -.05 C per day.  If the temperature continues to drop at this rate for 6 more days (a huge IF) before flattening out, then we’ll drop into ~-0.1 C  anomaly range for the remaining third of the month, and my guess will be landing pretty close.

Otherwise, and the scenario that is far more likely, is that my “system” will not be fail-proof.  Oh well.

AMRMo Finding a UHI Signal P3 – Using NOAA Population data

Recently, Zeke informed me of some nicely-formatted population data from NOAA for the U.S. going back to 1930.  Performing similar tests to Part 1 and Part 2 gives us an opportunity to use these extra years to search for any UHI bias.

Quick Note on Methods

Intermediate Data, Code, and Graphs for this post can be downloaded here.

“PopulationFinder” is the mini Java app that scans the specified folder for any DAT files, assumes they are in the NOAA format, and matches up the stations from USHCNv2 to their population as specified in the NOAA population files.  Basically, you can just download and unzip all the state population files into one directory and the PopulationFinder will do the heavy lifting.  The only thing that you can tweak here (and will be discussed later) is the  “MaxDistInKm” value, which will use all grid points within that distance to determine the average population for a station.  I’ve set it to 1.0 km, which means typically only 1-3 grid points are used.

One change I’ve subsequently made to the TempDataProcessor is how to determine if a station should be kept or not when performing the test.  Previously I just checked to make sure it reported avg temps at least 25 of the 31 years.  Now, with a longer time period, I want to make sure that every decade is represented, so it requires at least 7 years of reported avg temps from every decade.

I ran tests using the whole time period (1930-2000) and then just from 1970-2000 to compare the tests from Part 1 and Part2.

Results

Here are a couple of graphs for nearby stations using Raw and TOB datasets, but the remainder can all be found in the data/code/graph pack linked above.

Here is a quick summary of all the results from both 1930 on and 1970 on.

Discussion

Compare to our results from Part 2, and you’ll see that our correlations tend to be much worse and the slopes lower, especially in the same 1970-2000 period:

Results from NHGIS data in Part 2

So, if I’m assuming there is a strong enough signal to detect, here are some of my thoughts:

1. Lower threshold distance is better. This is kind of a no-brainer, since we’d think that nearby stations would have less actual climate-related differences.  We see that in almost all cases the < 0.5 degree distance shows better correlation and a higher slope.  Of course, some of this may be due to fewer observations, which is also a problem…there are not necessarily enough very close station pair candidates here.  I have a few ideas on how we might get more observations for this using a sliding time period window.  Once we get to higher thresholds, we start getting into the problem of spurious correlation due to trends in regions which I discussed previously.
2. The TOB datasets show the strongest signal.  Generally, they tend to do better than raw, which would be explained by the fact that they remove the noise from time of observation bias.  Of course, F52 does the worst by a good margin.  There are a couple explanations we might have for this.  According to NOAA on the F52 adjustments, “The U.S. HCN version 2 ‘pairwise’ homogenization algorithm addresses these and other issues…”  So, either these corrections
   1. Have “effectively account[ed] for any ‘local’ trend at any individual station”, thereby reducing the urban effect to something very small, as described here.  Or
   2. Have messed up any of our attempts to perform our comparison of nearby stations by already adjusting them to match other local stations.  This is not necessarily contrary to (A), if the UHI effect is indeed handled correctly.  However, if the corrections are based on faulty assumptions, then the waters have simply been muddied.  A closer examination of this is probably necessary.
3. There is more correlation than we would expect without any UHI signal.  However, there is clearly a lot of noise, and the magnitude of the effect so far seems to be on the smaller end.  As I’ve mentioned previously, I want to do a post dedicated to examining the magnitude of the effect.
4. Longer time frames bring out the signal better.  This is simply from comparing the 1930-2000 dataset to the 1970-2000 dataset for NOAA population data.  Makes sense if we’re reducing weather noise.
5. Using NHGIS “place” population data shows a stronger signal than the NOAA population data. There are once again a few different explanations here.  First, it may be that my data from NHGIS had fewer stations with population data, and that the ones it did have happened to show higher correlation.  It may also be that the NOAA data, since it is derived from county levels, is not as accurate in more rural areas as the NHGIS data for place (though I sort of doubt this).  Finally, it may be that the NOAA pop data IS more accurate for the grid points immediately surrounding a station, BUT that the “place” population is actually a better proxy for what goes into the UHI effect.  Maybe the development of the closest “place” actually biases a station more than simply the population density of its 1 square km area.

This leaves me with quite a bit to investigate.  Any feedback is of course welcome, especially from people that may have already been down this path.

AMRMo Finding a UHI Signal P2 – Increase vs decrease in population

In my last post (part 1), I performed the tests using the 1970-2000 population data from NHGIS and comparing the temperature trend and trend of log population of nearby stations in the USHCNv2 data set. 

One thing that has been nagging me is that while we might expect a population increase at a station to create a warming bias, I don’t expect a cooling bias of the same magnitude when we see a population decrease.  This is because we’re really attemping to use population in this case as a proxy for development using “urban” materials, and when a population decreases we don’t expect to necessarily lose any of these urban surfaces.  From the stations I used, about 35% of them actually had a population decrease over the period. 

Thus, my first test was to replace the dP value of any station < 0 with 0.  You can get the data (which is the same as last post) and the updated R file from here.  For you R programmers out there, I’d love to know how to do this more efficiently than using my for loop. 

One reason to be careful here is that this modification can greatly affect what we perceive to be the magnitude of the bias/effect.  After all, by replacing negative dPs with 0 we are decreasing our differences in the nearby station comparison, and thus increasing our dT/dP slope.  Furthermore, when it comes time to compute the population-adjusted temperature at each station to get our new average, we’ll be ignoring the cooling bias (if it exists) that might offset the warming bias. 

Also, since some of the UHI can be attributed to waste heat, we might expect at least that portion of it to decrease with a decrease in population.  After playing around with a couple different numbers, I settled on replacing dP with 1/4 * dP when dP is negative for a station.  Here are the tabled results between unadjusted, replacing negative dP with 0, and replacing negative dP with dP/4:

   

As you can see, in the tests above the best correlation seems to consistently appear when we use the 1/4 replacement.  However, it is somewhat troubling that the magnitude can be affected so much, with only slight differences in correlation.  Anyhow, here are some graphs with the 1/4 replacement.

A More Robust Method of Finding a UHI signal

This new iteration I’ve been working on in the background for a little while.  Previously, the correlation between the increase in temperature over a region and the coincidental increase in population density, along with the limited amount of population data, created a few stumbling blocks.

Basically, as in before, I want to examine how the change in population affects the station temperatures, since this change could theoretically occur in both rural and urban stations. See my original post here for more background.

Intermediate data and code for this post can be downloaded here.

New Population Data

Previously, I’ve been using GWPv3 for my population density data.  Unfortunately, this only included actual population data for the years 1990 and 2000 in the U.S.  However, aggregate U.S. census data for every decade can be downloaded from the
Nation Historical Geographic Information System.

There is perhaps a better way to do it, but after downloading the population data by “place” from the NHGIS data finder, I matched it to the various U.S. stations from the USHCN database using a combination of Excel macros and by hand.  (A sample macro for how I performed some of the mapping is included in the code above, as well as the population data by station for the years 1970, 1980, 1990, and 2000).  So now we at least have 3 decades of station population data to work with.

The Method

The temperature data I’m using is once again USHCNv2

1) For each station, the linear temperature trend (dT) is calculated based on the data from 1970-2000.  Similarly, we calculate the linear trend of the log of the population for the station (referred to as dP for simplicity) using the 1970, 1980, 1990, and 2000 population data. A station is only included IF at least 25 of its 31 years report annual temperature AND it has population for all 4 population years.

2) Based on latitude and longitude, we match all close station pairs.  (I should mention that Ron suggested something similar way back in an earlier comment).  For now I’ve matched based on “distance” in terms of degrees, which technically is not a valid physical distance, but should be close enough for this preliminary work.  The station pairs that are included are based on this “threshold” distance…I’ll show how this threshold affects various results below.  Obviously, the higher the threshold, the more station pairs we get.

3) We then graph these station pairs, plotting the difference in their linear temperature trends against the difference in their log population trends.  We should see a positive correlation if we believe population to be a proxy for UHI and that this effect is discernible in the station records.

Results – USHCN raw

Results – USHCN TOB Adjusted

Results – USHCN F52 Adjustments

Discussion

At first glimpse, this looks to me like there is indeed a UHI signal present based on population change.  All of the tests above seem to show at least some significant correlation.  This method seems to be fairly robust, but I’ve been wrong before.

On the other hand, it is hard to get a feel for the magnitude of this effect, since the slope varies wildly among each test.  Furthermore, even if we DO pick one of the higher ends, an early glance suggests the relative effect would not be very large compared to the temperature trend in the U.S. during the period.   I hope to do a more formal post investigating the magnitude of this effect in the future.

There are a number of other things I hope to do to help tease out the signal.  The population data per station I still feel is suspect, so I’m looking for ways to improve the accuracy at the actual station location.  Including more decades going back may also help eliminate some of the noise.  But perhaps what I’m most excited about are the other variables available for download at NHGIS, some of which include land use, which may be a better proxy for determining the magnitude of the UHI effect than population.

Explaining correlation in US UHI tests

Previously, I’d run a few tests and found a correlation between the change in population density from 1990 to 2000 and the change in temps from 1990 to 2000 in the US.  See here, here, and here.  At first I took this to be a UHI signal.  However, a bit more investigating has shown this is likely the result of a spurious correlation.  To summarize:  a large one-year swing in temps in a portion of the United States from 1989-1990 also happened to be in a similar area of the largest population growth from 1990-2000.  (Data and code available here).

Consider the now familiar graph I’ve shown multiple times:

However, what happens if we move back one year to the temperatures in 1989?  If what we’re seeing is a UHI signal, this should not have much of an effect, but…

Well, now we’re getting something nearly as strong in the opposite direction.  Clearly, much of this can be chalked up to the change in 1989-1990:

An extremely high correlation, but the population change from 1990 to 2000 obviously did not have an effect on the temperature change from 1989-1990.  In this case, I believe the explanation comes from geographic location.  Here’s an examination of how latitude and longitude correlate with the temperature swing from 1989-1990:

And now how lat/long correlate to the population change from 1990 to 2000.

The Story

To me the simple explanation is this — the Eastern U.S. heated up the most from 1989-1990.  This allowed for a generally larger temperature increase in the Western U.S. compared to what could be experienced in the East from 1990-2000 (since we already started on a peak for the East).  Meanwhile, it was the Western U.S. stations that experienced the largest relative population growth from 1990-2000.  Thus, we saw a correlation between the increase in temps and the population increase in the Western U.S., although in fact this had little to do with UHI. 

Betting on UAH Nov anomaly

Over at Lucia’s, she’s having her monthly betting game to determine the November anomaly for UAH.  I still haven’t won a single Quatloo over there, so I’m developing a can’t-fail system (gamblers out there know how this goes) to win some.

In one of the comments over there, somebody mentioned they would like to see SST and Aqua Ch. 5 daily anomalies from the AMSU website on the same graph, in order to determine the time lag between when SST begins to change and when the atmospheric temps go with it.   This sounded interesting and so I thought I’d try using the SST temps to guess the Nov UAH anomaly.

First, we have our graph with SST and Aqua ch.5 data plotted together:

Also one with SSTx3 to help show the lag:

So, we can see that generally SST falls and then the Aqua temps follow, but for a prediction we’ll need a better estimate of the actual lag time.  I thus tried (or rather, a Macro tried) lag times between 0-200 days for Aqua ch.5 data and attempted to see which resulted in the best correlation.  First, for all days since 2003:

In this case, our best R is 0.683, and it occurs at 49 days.

However, we can see that the lag time appears to be longer in the big peaks and troughs more recently, so I went ahead and tried everything from 2006-Present:

Here, we get our best correlation of 0.766 at 112 days, which is a substantial change from before.  Finally, I went ahead and tried with only the most recent years (2008 – present):

Here, we get our best R=0.811 at 87 days.

From these graphs, clearly we have a wide range of lag times to choose, and so this “system” will be far from exact.  My general impression from the graphs is that during large dips the lag time is longer, and so I’m going to go forward with the 112 day lag time for this La Nina.  Furthermore, I’m going to take the slope of 1.57 that we find between the SST and AquaCh5 data when using the 112 day lag.

Our new graphs (the first is 2006-Present only) show a better match-up:

The actual prediction: 0.118 C

The 112 day lag puts us back at days 2755 through 2784 for SST, which yields an average anomaly of 0.021.  Multiplying this by our slope of 1.57 yields 0.033 C.  But this is relative to our 2003-2009 November baseline.  The UAH anomaly is reported relative to the 1979-2009 baseline.  The 1979-2009 November baseline is actually 0.085 lower.  Thus, we have 0.033 + 0.085 = 0.118.

Other Notes:

-This estimate was actually to determine what the average daily anomaly for November in the Aqua ch5 data would be…I’m not sure exactly how well this corresponds to the reported UAH anomaly. 

-According to the AMSU website, the temps having actually been climbing pretty quickly for the first few days of Nov, once again calling into question the guarantee of this can’t-fail system…

Summary of US UHI tests with all datasets

Continuing the work from before (most recently here), I went ahead and modified the java code to handle a variety of new formats for different temperature datasets.  Here I’ll be basically performing the same tests I’ve done before, but will add in tests with a couple new datasets — GHCN v3 beta and Ron Broberg’s GSOD work.

Data Everywhere

My code and intermediate data available HERE (I manually extracted all US-stations from the global list using Excel).

Other relevant data: GHCNv2 , USHCNv2, GSOD,  GHCNv3 (beta), GWPv3 (population data)

Changes to Calculation Method

Previously, I’ve been using (Pop2000-Pop1990) / (Pop2000) for the changing population X-axis value.  This was a rather boneheaded move because clearly this gives an inflated value for a decrease in population vs. an increase.  From here on out I’ll be using a more sensible calc of  (Pop2000-Pop1990) / (Pop2000+Pop1990)

Summary Table

As you can see, the “signal” appears far stronger in all of the HCN data sets than in the GSOD data set.  This could simply be because all of them share many of the same stations, and hence a fluke.  What’s also interesting is that the adjusted data sets all have a higher correlation and slope than their counterparts.  As I’ve suggested before, I don’t believe this is because the adjustments are adding in more UHI errors — rather, I think they are clarifying other errors, which only makes the UHI signal come in clearer.  This may explain the low correlation in the GSOD data set, which clearly has the least amount of QC.

Notes

-The graphs below will show a slope 10x more for GHCNv3 than for the other data sets, because they report in hundredths of a degree instead of tenths.

-For calculating yearly anomalies for the global data sets, I’ve once again required 12 months of reported data.

Graphs