Effective vs. Equilibrium Sensitivity: Uncertainty in projections resulting from the CMIP5 OHU efficacy range in a two-layer model

A somewhat frequent topic that has come up here has been the difference between effective sensitivity and equilibrium sensitivity; that is, the extent to which the increase in outgoing radiative flux per unit increase in temperature may change over time.  Given the timescales involved, the relationship between “effective” sensitivity calculated over some transient time period (typically 100-200 years) and equilibrium sensitivity is nearly impossible to observe in the real world, so experiments so far have been primarily model-based, such as in Armour et al, 2013 and Rose et al., 2014.  The abstract of the latter study concludes with: “Results imply that…equilibrium climate sensitivity cannot be reliably estimated from transient observations.”  While certainly interesting from an academic perspective, I have found myself wondering whether this result is actually relevant to projection of future anthropogenic warming.  After all, if “effective” sensitivity (EFS), which is calculated on century timescales, significantly deviates from equilibrium sensitivity (ECS, which applies to millennial timescales), then it would seem to suggest that EFS should be the focus when determining policy / projections. 

One way to model this contrast in EFS vs. ECS is using a factor for “efficacy” (not “efficiency”, which is a separate concept) of ocean heat uptake (OHU), per Winton et al., 2010 and Held et al., 2010.  In Geoffroy et al., 2013 Part II (the first part of which I’ve been referencing for my two-layer model), the authors indicate that such a two-layer model with this efficacy factor is generally able to represent the global behavior of the CMIP5 AOGCMs:

 

and

 

Here C and C_0 represent the heat capacities of the atmosphere+ocean mixed layer and deeper ocean respectively, T and T_0 represent the temperature anomalies for those layers, gamma represents the heat transfer rate between those layers, epsilon represents the efficacy of ocean heat uptake, F represents the TOA forcing, and lambda represents the equilibrium radiative restoration strength. 

Anyhow, using this representation suites my purpose here, as I want to isolate the uncertainty in the RCP projections that might result exclusively from the uncertainty in this efficacy parameter.  Essentially, I want to answer this question: if we remove almost all uncertainty from the magnitude/efficacy of forcings, temperature observations, natural variability, and TOA imbalance, such that  we could constrain the TCR and EFS calculated from 1860-1879 to 2000-2009 to 1.4 K +/- 0.05 and 2.0 K +/- 0.05 respectively (similar to the most likely estimates of Otto et al. (2013)), what sources of uncertainty would remain for the respective RCP scenario projections?  In this two-layer model, there are three parameters that can be tuned if we assume ECS = EFS while constraining to the TCR=1.4 and EFS=2.0 calculations mentioned previously: C, C_0, and gamma.  As there is no unique solution set, I only sample from the range of values calculated in Geoffroy et al., 2013 for the CMIP5 AOGCMs for each of the parameters, which still yields a large ensemble of models (that is, parameter combinations).  Now, if we don’t assume ECS = EFS, we can vary two more parameters: efficacy and lambda.  Once again I constrain efficacy to be within the range of values calculated by  Geoffroy et al., 2013 for that set of AOGCMs, while allowing lambda to be a “free” parameter.  This obviously gives a larger ensemble of models than when only allowing the ocean parameters to be modified. 

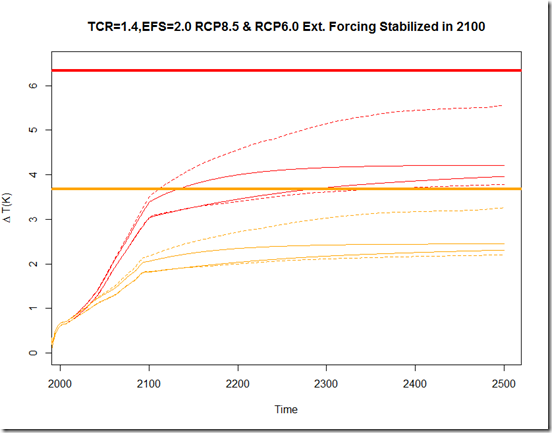
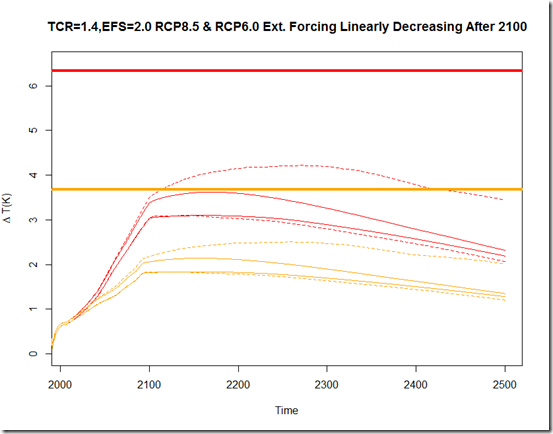
The next step is to run these models with the adjusted RCP forcings calculated in Forster et al., 2013.  I have extended these forcing beyond 2100 using two simple scenarios: the first is to maintain the forcing in 2100 through 2500, while the second linearly decreases the forcing from 2100 to 2500 so that the value in 2500 is half (relative to pre-industrial) of what it was in 2100.  From here, if we compare the 2.5%-97.5% interval from the only-ocean-modified-parameters ensemble (solid lines) with that of the efficacy-modified ensemble (dashed lines), we can see the practical difference in EFS vs. ECS in these future projections.  These first two figures show the aforementioned scenarios for RCP8.5 (red) and RCP6.0 (orange), with the thick lines representing the equilibrium temperature response to the scenario forcing if ECS=3.0 (noting that the dashed 97.5% upper-limit essentially represents a model with an ECS=3.0 and EFS=2.0).

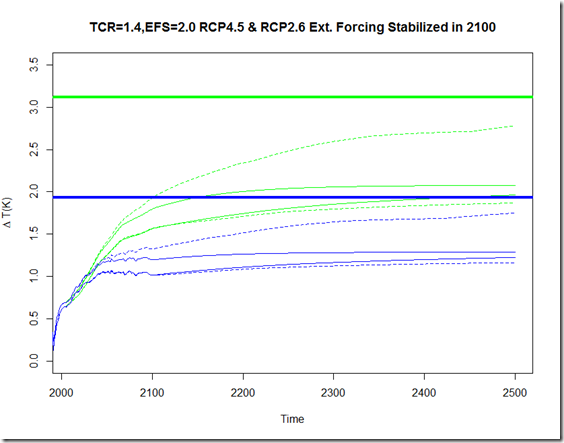
And these next two figures show the same thing for RCP4.5 (green) and RCP2.6 (blue):

 

As can be seen, the uncertainty from the efficacy of OHU does not really manifest itself prior to 2100 in the projections.  Beyond that, the high-end uncertainty increases for the varying-efficacy ensemble relative to the fixed efficacy model, although the behavior largely depends on the behavior of the forcings after 2100.  In the event that these forcings are fixed for the subsequent 400 years, the high-end efficacy separates itself from the effective sensitivity path and continues marching towards the equilibrium temperature change.  In the event that the forcings begin to decrease after 2100, even the high-end efficacy never comes particularly close to its equilibrium change.

I should note that not too much should be made about the asymmetric nature of the varying-efficacy uncertainty bounds.  This is a consequence of simply using a uniform sampling of efficacy from the range of CMIP5 models (0.8 – 1.8), and obviously since an efficacy > 1.0 implies an ECS > EFS, we are grabbing higher-up in the efficacy range.  Whether these CMIP5 AOGCMs represent a reasonable range for the efficacy is a reasonable question, but I’m not sure it has an easy answer.    

Script is available here.