Does the Shindell (2014) apparent TCR estimate bias apply to the real world?

There has been some considerable discussion of Shindell (2014) and the suggestion that usual estimates of TCR (which assume roughly equal efficacies for different forcings), such as Otto et al, (2013), might be underestimating TCR with the traditional method.  A few example discussing Shindell (2014) are at Skeptical Science, And Then There’s Physics, and Climate Audit.  SkS’s Dana went so far as to say the paper “demolishes” Lewis and Crok’s report at James Annan’s blog, but JA responds quite skeptically of the Shindell (2014) results.

On the face of it, the argument is fairly simple and intuitive (so buyer beware!): since the cooling effect of aerosols generally occur in the Northern Hemisphere where there is greater land mass and thus lower effective heat capacity, these forcings will disproportionally affect the global temperature relative to the forcing of well-mixed greenhouse gases, which acts globally.  Since Watt per Watt these cooling forcings will give you more bang for your buck, an estimate of TCR using only the globally averaged forcing and global temperature could be biased low.  Shindell (2014) therefore tries to find the average “enhancement” of aerosol+O3 forcings, E, through GCMs, and uses the following to calculate TCR from global quantities:

TCR = F_2xCO2 x (dT_obs / (F_ghg + E x (F_aerosols + F_Ozone + F_LU)))

However, there are reasons to be skeptical of this result as well.  For one, there *have* been studies that specifically looked at the rate of warming and certainly don’t assume homogenous forcings, such as Gillett et al (2012), which find low TCR estimates consistent with Otto et al., (2013).  Furthermore, Shindell (2014) does not seem to consider the ratio of observed warming in the NH vs. SH. ..using Cowtan and Way (2013) with HadCRUT4 kriging, from the base period (1860-1879) through the end of the historical simulation time period (1996-2005), the ratio of NH warming to SH warming is 1.48.  Obviously, if there was a large cooling effect from aerosols concentrated primarily in the NH (due to a large enhancement of the aerosol effect), we would expect to see more warming in the SH than the NH!  Third, there did not seem to be any tests run on the actual historical simulations from models, which would tell us how well the Shindell (2014) method performs relative to the “simple” E=1.0 method (e.g. Otto et al).  These last tests should be easy to pass, since the value of “E” would be calculated from the same model that the tests are run on (unlike the real world, where we don’t know the “true” value of E).

The first table simply shows the forcings and temperature changes using the same models as S14, as much of this information is available in the supplement.  These tests will be based on the difference between the base period (1860-1879) and the end of the historical simulation (1996-2005) using the historical runs.

TABLE 1. Temperature + Forcing from historical simulations and Aero/O3 Enhancement (from Shindell 2014)

Model	ΔT	ΔF_WMGHG	ΔF_Aero_O3_LU	ΔF_2xCO2	E
IPSL-CM5-LR	1.15	2.40	-0.45	3.20	2.43
CanESM2	0.94	2.40	-0.69	3.70	1.18
GFDL-CM3	0.49	2.49	-1.12	2.99	1.57
CSIRO-MK-3.6.0	0.58	2.15	-1.13	3.10	1.18
HadGEM2-ES	0.53	2.27	-1.08	3.50	1.48
MRI,NOR,MIROC AVG	0.56	2.05	-0.83	3.65	1.40

One thing that has been nagging me about this is that natural forcings are not included in the TCR equation above.  I am not sure if the slightly positive solar influence is balanced out by the slightly negative volcanic influence in models, or what, but S14 does not include estimates of these natural forcings in the models so I have not included them in the tests either. And here are the results of the actual tests using the above numbers: 

TABLE 2. Estimate of TCR using Simple (E=1.0) estimate vs. Shindell (2014) methods, along with NH/SH warming ratios

Model	Simple Estimate (K)	Shindell Estimate(K)	TCR Actual (K)	Error_Simple	Error_Shindell	NH/SH Hist	NH/SH HistGHG
IPSL-CM5-LR	1.88	2.79	2.00	-6%	40%	1.49	1.62
CanESM2	2.03	2.19	2.40	-16%	-9%	0.96	1.28
GFDL-CM3	1.07	1.98	2.00	-47%	-1%	0.84	1.90
CSIRO-MK-3.6.0	1.75	2.19	1.50	17%	46%	1.00	1.15
HadGEM2-ES	1.56	2.75	2.10	-26%	31%	1.17	1.70
MRI,NOR,MIROC	1.67	2.28	1.70	-2%	34%	1.58	1.60
Observed (CW13)						1.48

Assuming I have not messed something up here, these results appear to be very concerning for Shindell (2014).  For example, IPSL-CM5-LR, the model from S14 with the largest “enhancement” at E=2.43, would be expected to yield a major underestimate of TCR using the simple method.  Instead, the simple estimate only underestimates TCR by 6%, whereas applying the S14 “correction” makes things far worse, yielding a 40% overestimate of TCR!  In fact, in 4 of the 6 models, the Shindell method overestimates the TCR by > 30%.  On the other hand, the “simple” method only underestimates TCR by > 30% in 1 of the 6 cases.  

Perhaps even more concerning, however, is the specific model ensembles for which the Shindell (2014) method largely overestimates the TCR.  Given the observed NH/SH warming ratio of 1.48, the two models that are most realistic in this regard are IPSL-CM5-LR (1.49) and the average of MRI, NOR, and MIROC (1.58).   Since the argument from Shindell (2014) essentially hinges on the NH being disproportionately cooled by aerosols relative to the SH, these are the most directly relevant.  And yet, using the “simple” method in these cases produces underestimates of 6% and 2%, which would hardly change the results of a paper like Otto et al, 2013.  On the other hand, the Shindell (2014) “correction” causes overestimates of 40% and 34%  (e.g. a shift from a 1.3K “most likely” value from Otto to the 1.7K reported by S14).  If we look at the model that the “simple” method largely underestimates, GFDL-CM3, we see that the 0.84 NH/SH in that model is the farthest away from the one we’ve observed in the real world, suggesting it is likely the least relevant. 

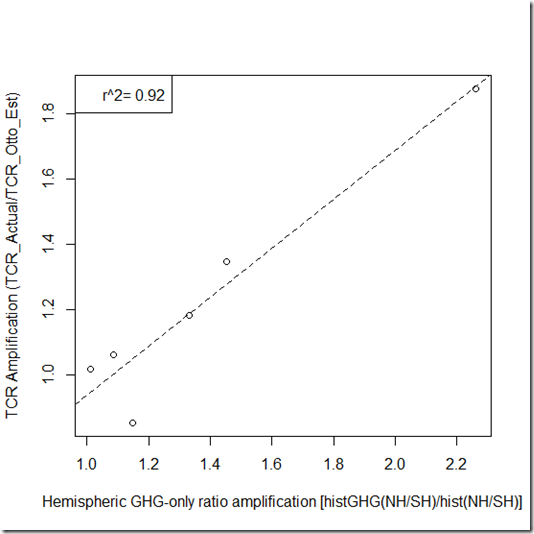
In fact, I would argue that the amplification of the NH/SH ratio in the historicalGHG simulation relative to the historical simulation for a model could be used to better estimate the TCR “bias” calculated using that model.  This is because the difference in the NH/SH ratio in the historicalGHG simulation and that of the historical simulation implicitly combines the actual aerosol forcing and the “enhancement” of this forcing (rather than trying to estimate these highly uncertain values separately), which is even more directly relevant to the degree of TCR bias.  Indeed, if we look here, there appears to be excellent correlation:

 

 

Impressive, eh?   Now, I will mention that I believe things to be less pretty than the r^2=0.92 value shown above.  This is primarily because the 3 models bundled in Shindell et al (2014) actually have very different rates of global warming, as well as the NH/SH ratios, so I’m not sure it makes sense to bundle them, but have done so here for consistency with S14. 

One problem with using my method here and applying it to the“real-world”  is that we don’t know what the NH/SH warming ratio would be for the real world in the GHG-only scenario.  However, given the high value of 1.48 observed for the real-world “all-forcing” case, I suspect that the difference between this ratio and the GHG-only scenario can’t be that large, unless models have seriously underestimated the historicalGHG warming ratios.  Moreover, I would argue that the value is likely to be better constrained from models than the value of E, which depends on the much more uncertain aerosol properties.   Regardless, the average model warming ratio for NH/SH for the historicalGHG simulations in the above models is 1.54.  If you plug in the observed value of 1.48 for the “historical” observed NH/SH ratio in the real world, and use the linear regression from above, the estimated TCR bias amplification factor is 0.96.  This would suggest using the “simple” method slightly overestimates TCR, but by an extremely small fraction. 

Conclusion

While Shindell (2014) uses several GCM results to argue that traditional methods to calculate TCR lead to an underestimate, testing these methods against the outputs of those same GCMs seems to suggest the “simple” (E=1.0) methods perform better than the S14 “corrected” method.  Furthermore, when we consider the actual observed NH/SH warming ratio, it also seems to suggest that the TCR bias in the traditional/simple method is either very small or non-existent. 

Data and code.

How sensitive are the Otto et al. TCR and ECS estimates to the temperature and ocean heat datasets?

There seems to have been some interest in the sensitivity of Otto et al. (2013) lately.  For instance, see Piers Forster’s comments about HadCRUT4 in Otto, or Trenberth and Fasullo (2014), which notes that using ORAS-4 for the OHC dataset raises the estimate of ECS from 2.0 to 2.5 K.   Anyhow, I ran a few of the tests, and thought I would share the results. 

Otto et al (2013) uses five different intervals over which the differences of temperature, forcing, and TOA imbalance (for the ECS estimate) are calculated: 1) 2000s – Base, 2) 1990s – Base, 3) 1980s – Base, 4) 1970s – Base, and 5) the 40 year interval from 1970-2009.  The base period used is 1860-1879.  Here are the results when using the BEST or Cowtan and Way (2013) global temperature datasets (which infill under-sampled regions to get more global coverage)  to calculate TCR alongside HadCRUT4:

 

	ΔF (W/m^2)	HadCRUT4 ΔT (K)	HadCRUT4 TCR (K)	CW13 ΔT (K)	CW13 TCR (K)	BEST ΔT (K)	BEST TCR (K)
2000s-Base	1.94	0.75	1.33	0.81	1.44	0.81	1.44
1990s-Base	1.25	0.57	1.57	0.6	1.65	0.6	1.65
1980s-Base	0.99	0.39	1.36	0.43	1.49	0.44	1.53
1970s-Base	0.75	0.22	1.01	0.26	1.19	0.27	1.24
2009-1970	1.28	0.53	1.42	0.56	1.51	0.54	1.45

In most situations, it appears that the difference is relatively small, adding ~0.1K of TCR when using either Cowtan and Way (2013) or BEST global temperatures.    
   
For ECS, I used Cowtan and Way (2013) for the temperature dataset and three different ocean heat content datasets: 1) Lyman and Johnson (2014), 2)  ORAS-4, the reanalysis product introduced in Balmaseda et al. (2013), and 3) Levitus et al (2012).  For #1 and #2, I digitized the values from their respective papers.  Since the calculation of ECS is slightly more complicated, I have included additional steps along the way.  OHU represents the rate of ocean heat uptake as calculated over the period from the observed ocean heat content,  and ΔQ represents the change in TOA imbalance over the interval (I assume 90% of the TOA imbalance goes into the ocean, and per Otto et al that the imbalance of the base period was 0.08 W/m^2).  I also include a “most recent” period calculation, which occurs if we measure the OHC after the bulk of the ARGO deployment took place.  For LJ14 they present this value from 2004-2011.  For L12, they don’t present annual estimates until 2005, so I’ve used 2005-2013.  For B13, I simply used 2004-2010.  Here are the results:

 

	ΔF (W/m^2)	CW13 ΔT (K)	LJ14 OHU (W/m^2)	LJ14 ΔQ (W/m^2)	LJ14 ECS (K)	B13 OHU (W/m^2)	B13 ΔQ (W/m^2)	B13 ECS(K)	L12 OHU (W/m^2)	L12 ΔQ (W/m^2)	L12 ECS (K)
2000s-Base	1.94	0.81	0.50	0.48	1.90	0.85	0.86	2.59	0.48	0.45	1.87
1990s-Base	1.25	0.60	0.25	0.20	1.96	-0.22	-0.32	1.31	0.25	0.20	1.96
1980s-Base	0.99	0.43	-0.26	-0.37	1.09	0.49	0.46	2.81	0.13	0.06	1.60
1970s-Base	0.75	0.26	0.32	0.28	1.89	0.16	0.10	1.37	0.49	0.46	3.13
2009-1970	1.28	0.56		0.20	1.78		0.77	3.75		-0.01	1.49
Post_ARGO(2004 or 2005)-Base	1.94	0.85	0.29	0.24	1.72	0.51	0.49	2.01	0.54	0.52	2.06

As you can see, the bulk of the estimates still seem to suggest an ECS < 2K, in line with the Otto et al (2013) calculations.  For LJ14, the results are actually pretty tightly constrained (apart from the “low-ball” 1980s estimate) between 1.7 and 2.0 K.  Using ORAS-4 (B13) does increase the ECS estimate when using the 2000s only, but it also largely decreases when using the 1990s or 1970s.  When using only post-ARGO data, it is pretty much in line with the others, suggesting an ECS ~ 2K.  L12 is also fairly tightly constrained, apart from the “highball” estimate of the 1970s.  Overall,using ORAS-4 produces the largest error margins and interval-specific sensitivity. However, it is worth noting that using the post-ARGO OHC data seems to largely remove the dependence on which OHC dataset is chosen, producing best estimates between 1.7 and 2.1 for ECS. 

Data for this post available here.