On forcing enhancement, efficacy, and Kummer and Dessler (2014)

A paper by Kummer and Dessler (2014) [KD14] has recently been accepted by GRL, with the primary claim being that observational estimates of ECS over the 20th century can be reconciled with the higher ECS of CMIP5 models by accounting for the “forcing efficacy” mentioned in Shindell (2014):

Thus, an efficacy for aerosols and ozone of ≈1.33 would resolve the  fundamental disagreement between estimates of climate sensitivity based on the  20th-century observational record and those based on climate models, the paleoclimate record, and interannual variations.

However, I think there is some fundamental confusion with respect to how the forcing enhancement should be applied within KD14, which I will focus on specifically for this post (ignoring what I believe to be other issues in the actual energy balance calculations for the mean time).  While I have noted previously that the spatial warming pattern appears to indicate a value of “E” (the Shindell enhancement) near unity, I would submit that even if it was significantly greater than 1.0, it has been applied in a way within KD14 that likely substantially exaggerates its effect on 20th century ECS calculations.  Here are the issues that I see:

1. ECS calculations are unaffected by the effective heat capacity, whereas TCR calculations are not

First, let’s take a look at the Shindell (2014) definition for the forcing enhancement (which KD14 refers to as “forcing efficacy”), which is the ratio of the inhomogenous forcing TCR to that of the homogenous forcing TCR:

(Eq. 1)        

TCR is calculated by dividing the temperature change by the forcing, without consideration of the TOA energy imbalance at the time of the calculation (this is often normalized to transient change for a doubling of CO2 by multiplying by F_2xCO2 (~3.7 W/m^2), but I will leave it simply in the units of K/(W/m^2) for this post):

(Eq. 2)       

And if we consider the simple one box temperature response to an imposed forcing at time t, we have:

(Eq. 3)      

Where F is the imposed forcing change, lambda is the strength of radiative restoration (the increase in outgoing flux per unit of surface warming), and C is the effective heat capacity of the system.  As can be seen by working back from equation 3 to 1, TCR and hence E  will be affected by both the difference in C (the heat capacity) and lambda (radiative restoration) between the homogenous and inhomogeneous forcings.  On the other hand, the equilibrium response (t –> infinity) to a forcing does NOT depend on C, only lambda.

If we go back to the simple energy balance equation for the top of the atmosphere (TOA) , re-arranging eq. 1 in KD14 to solve for lambda (with N representing this net TOA imbalance), we have:

(Eq. 4)     

which can then be inverted and multiplied by F_2xCO2 to find the ECS in terms of a CO2 doubling.  What should be quite clear from this determination of ECS is that one can dampen the transient temperature response by increasing the value of C without it affecting the estimate of ECS.  After all, If the temperature response is heavily damped in the first 50 years for a forcing (due, for example, to the bulk of that forcing being concentrated in an area with deep oceans), then it is true that the value for T will be lower than it might be for a scenario with less ocean damping, but  the TOA imbalance (N) will be larger due to less radiative response (from lambda * T), thereby decreasing the quantity (F-N) by the same ratio , and yielding the same value for lambda.  On the other hand, it is clear why such ocean damping *would* affect the TCR, which does not take into account the TOA imbalance (N).

The problem should thus be obvious: the “enhancement” factor calculated by Shindell (2014) can be greatly affected by the difference in effective heat capacity of the hemispheres, but this in itself would not create any bias in the ECS calculations.  So KD14 should certainly not be using the forcing “enhancement” factor of Shindell as a proxy for the equilibrium forcing efficacy!  Note that much discussion regarding Shindell (2014) focused on how the greater land mass of the NH corresponds to a lower heat capacity, thus producing a greater transient response for an aerosol forcing located primarily in the NH.   But this intuition has nothing to do with a bias in the equilibrium response.

Rather, as I mentioned above, E is affected by both the effective heat capacity differential (C) and the increase in outgoing flux per unit increase in temperature (lambda), only the latter of which actually affects ECS.  So the more we find that E is a result of the differing heat capacity, the less room that leaves for lambda to have a substantial effect, and the less bias this would actually produce in the ECS estimates.  Furthermore, there seems to be less of the way in intuition of why a differing lambda would be responsible for a substantial portion of E, if this were the case.  Nevertheless, it IS possible that for a larger E, at least some portion of this would come from a differing radiative response strength from homogenous and inhomogenous forcings, but that leads to the second issue…

2. The Forcing Efficacy “correction” in the estimate is applied directly to the TOA imbalance resulting from the forcing, thereby overcompensating in transient estimates

Per KD14, we read that:

To test the impact of efficacy on the inferred λ and ECS in our calculations, we multiply the aerosol and ozone forcing time series by an efficacy factor in the calculation of the total forcing.

What Kummer and Dessler (2014) have done here is simply inflated the magnitude of the aerosol and ozone forcings beyond the best estimates, rather than actually accounting for the forcing “efficacy” that may result from differing lambdas.  In the event that the TOA imbalance has already reached equilibrium, there is no need for this distinction.  But in transient runs, using the KD14 method will bias the ECS high, because it is compensating for the differing TOA response in the numerator of Eq. 4 that has not yet fully manifested!

Consider an example, where lambda is 1.5 W/m^2/K for GHG (~2.5 K “true” ECS), but the “forcing efficacy” for aerosols is 1.5 and entirely comes from differing lambda, such that lambda for aerosols is 1.0 W/m^2/K.  Now suppose we perform our calculation early on in the transient run, such that only 50% of the equilibrium response to a given forcing of 2.0 W/m^2 GHG and –1.0 W/m^2 aerosols has been achieved.  This will yield T_GHG = 2.0 / 1.5 * 50% = 0.67 K, and T_aero = –1.0 / 1.0 * 50% = –0.5 K, for a net T of 0.17 K.  Using the KD14 method with Eq. 4, we would have an F = 2.0 W/m^2 – 1.5 * 1.0 W/m^2) = 0.5 W/m^2, an N of (2.0 W/m^2 – 1.0 W/m^2)  – [0.67 K * (1.5 W/m^2/K) + (-0.5 K) * (1.0 W/m^2/K) ]= .495 W/m^2, leading to a lambda of (0.5 – 0.495) / (0.17 K) = 0.03 W/m^2/K, corresponding to a sensitivity of > 100K!  This extreme example highlights the large bias that the KD14 method can produce when applied to transient runs.  Currently, if one takes the last decade net TOA imbalance to be ~ 0.6 W/m^2, and the forcing up to now to be ~ 2.0 W/m^2, this implies we are about 70% equilibrated…under these circumstances I would still expect a large bias from the KD14 application.

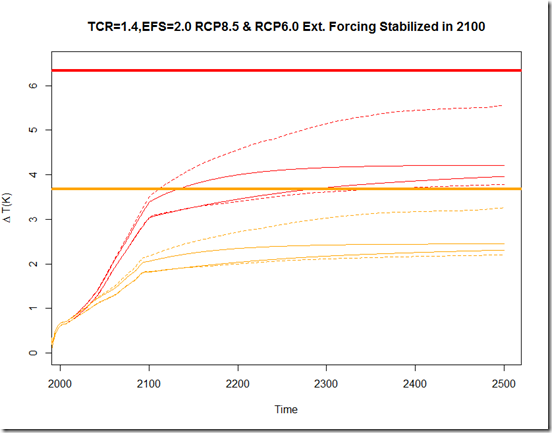
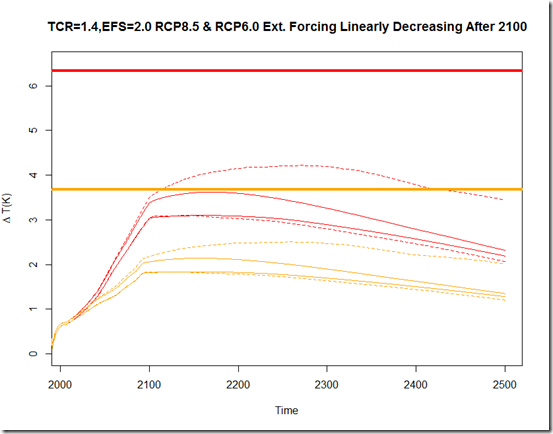
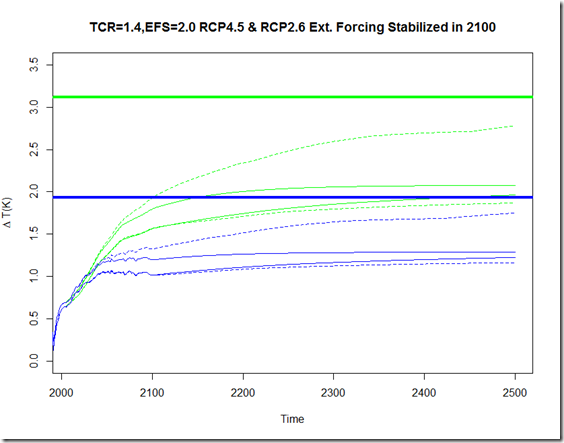
Anyhow, to illustrate the bias we would expect from the different methods of calculating ECS given an E of 1.5, I have written a script here.  Essentially, it treats the two hemispheres as separate one-box models, with the historic non-GHG anthropogenic forcings applied entirely to a more sensitive NH.  I have tried to match this to some degree so that the ending TOA imbalance is around 0.5 W/m^2 (and hence around 70% equilibrated), similar to that observed, but it is also possible that these models have oversimplified things.  Nevertheless, here are the results:

What this illustrates is much of the intuition we have gone over in these two sections.  From the blue line, we see that as we increase the attribution of the calculated E  to the heat capacity differential, there is very little bias introduced when calculating ECS using the “traditional” energy balance method (per #1 above, this is because there is less attributable to the difference in lambda) .  On the other hand,  since we introduce a case here where we are still far from equilibrium, the KD14 method creates an overestimate in all cases.

Summary

Overall, I am quite dubious about the KD14 results, for 3 reasons:

1) Based on the observed spatial warming, it seems unlikely that E is far from unity.

2) Even if E were greater than 1.0, only a fraction of that E applies to ECS estimates (the portion stemming from differential lambdas and NOT heat capacities), and

3) Even if the full E did apply, it appears KD14 has applied it incorrectly, introducing a large overestimate in the transient cases

The shame of it all is that this actually hints at an interesting underlying question, which is whether the spatial pattern of warming in the real world has created a radiative response substantially different from the response expected from a uniform GHG forcing.  It seems that if one were interested in what models say, however, it could be calculated much more directly – comparing the AMIP simulated radiative restoration strength to that of the historicalGHG from the same models would likely be the way to begin along this path.

Effective vs. Equilibrium Sensitivity: Uncertainty in projections resulting from the CMIP5 OHU efficacy range in a two-layer model

A somewhat frequent topic that has come up here has been the difference between effective sensitivity and equilibrium sensitivity; that is, the extent to which the increase in outgoing radiative flux per unit increase in temperature may change over time.  Given the timescales involved, the relationship between “effective” sensitivity calculated over some transient time period (typically 100-200 years) and equilibrium sensitivity is nearly impossible to observe in the real world, so experiments so far have been primarily model-based, such as in Armour et al, 2013 and Rose et al., 2014.  The abstract of the latter study concludes with: “Results imply that…equilibrium climate sensitivity cannot be reliably estimated from transient observations.”  While certainly interesting from an academic perspective, I have found myself wondering whether this result is actually relevant to projection of future anthropogenic warming.  After all, if “effective” sensitivity (EFS), which is calculated on century timescales, significantly deviates from equilibrium sensitivity (ECS, which applies to millennial timescales), then it would seem to suggest that EFS should be the focus when determining policy / projections. 

One way to model this contrast in EFS vs. ECS is using a factor for “efficacy” (not “efficiency”, which is a separate concept) of ocean heat uptake (OHU), per Winton et al., 2010 and Held et al., 2010.  In Geoffroy et al., 2013 Part II (the first part of which I’ve been referencing for my two-layer model), the authors indicate that such a two-layer model with this efficacy factor is generally able to represent the global behavior of the CMIP5 AOGCMs:

 

and

 

Here C and C_0 represent the heat capacities of the atmosphere+ocean mixed layer and deeper ocean respectively, T and T_0 represent the temperature anomalies for those layers, gamma represents the heat transfer rate between those layers, epsilon represents the efficacy of ocean heat uptake, F represents the TOA forcing, and lambda represents the equilibrium radiative restoration strength. 

Anyhow, using this representation suites my purpose here, as I want to isolate the uncertainty in the RCP projections that might result exclusively from the uncertainty in this efficacy parameter.  Essentially, I want to answer this question: if we remove almost all uncertainty from the magnitude/efficacy of forcings, temperature observations, natural variability, and TOA imbalance, such that  we could constrain the TCR and EFS calculated from 1860-1879 to 2000-2009 to 1.4 K +/- 0.05 and 2.0 K +/- 0.05 respectively (similar to the most likely estimates of Otto et al. (2013)), what sources of uncertainty would remain for the respective RCP scenario projections?  In this two-layer model, there are three parameters that can be tuned if we assume ECS = EFS while constraining to the TCR=1.4 and EFS=2.0 calculations mentioned previously: C, C_0, and gamma.  As there is no unique solution set, I only sample from the range of values calculated in Geoffroy et al., 2013 for the CMIP5 AOGCMs for each of the parameters, which still yields a large ensemble of models (that is, parameter combinations).  Now, if we don’t assume ECS = EFS, we can vary two more parameters: efficacy and lambda.  Once again I constrain efficacy to be within the range of values calculated by  Geoffroy et al., 2013 for that set of AOGCMs, while allowing lambda to be a “free” parameter.  This obviously gives a larger ensemble of models than when only allowing the ocean parameters to be modified. 

The next step is to run these models with the adjusted RCP forcings calculated in Forster et al., 2013.  I have extended these forcing beyond 2100 using two simple scenarios: the first is to maintain the forcing in 2100 through 2500, while the second linearly decreases the forcing from 2100 to 2500 so that the value in 2500 is half (relative to pre-industrial) of what it was in 2100.  From here, if we compare the 2.5%-97.5% interval from the only-ocean-modified-parameters ensemble (solid lines) with that of the efficacy-modified ensemble (dashed lines), we can see the practical difference in EFS vs. ECS in these future projections.  These first two figures show the aforementioned scenarios for RCP8.5 (red) and RCP6.0 (orange), with the thick lines representing the equilibrium temperature response to the scenario forcing if ECS=3.0 (noting that the dashed 97.5% upper-limit essentially represents a model with an ECS=3.0 and EFS=2.0).

And these next two figures show the same thing for RCP4.5 (green) and RCP2.6 (blue):

 

As can be seen, the uncertainty from the efficacy of OHU does not really manifest itself prior to 2100 in the projections.  Beyond that, the high-end uncertainty increases for the varying-efficacy ensemble relative to the fixed efficacy model, although the behavior largely depends on the behavior of the forcings after 2100.  In the event that these forcings are fixed for the subsequent 400 years, the high-end efficacy separates itself from the effective sensitivity path and continues marching towards the equilibrium temperature change.  In the event that the forcings begin to decrease after 2100, even the high-end efficacy never comes particularly close to its equilibrium change.

I should note that not too much should be made about the asymmetric nature of the varying-efficacy uncertainty bounds.  This is a consequence of simply using a uniform sampling of efficacy from the range of CMIP5 models (0.8 – 1.8), and obviously since an efficacy > 1.0 implies an ECS > EFS, we are grabbing higher-up in the efficacy range.  Whether these CMIP5 AOGCMs represent a reasonable range for the efficacy is a reasonable question, but I’m not sure it has an easy answer.    

Script is available here.