How well do the IPCC’s statements about the 2°C target for RCP4.5 and RCP6.0 scenarios reflect the evidence?

1. Introduction

In the IPCC AR5 summary for policy makers (SPM), there are few statements that are likely to garner more attention than those related to projected warming for this century under various scenarios.  In particular, given the prominence placed on the 2 degrees Celsius target, I would argue that Section E.1 is of great importance for policy makers. In the top box, we read:

Global surface temperature change for the end of the 21st century is likely to exceed 1.5°C relative to 1850 to 1900 for all RCP scenarios except RCP2.6. It is likely to exceed 2°C for RCP6.0 and RCP8.5, and more likely than not to exceed 2°C for RCP4.5.

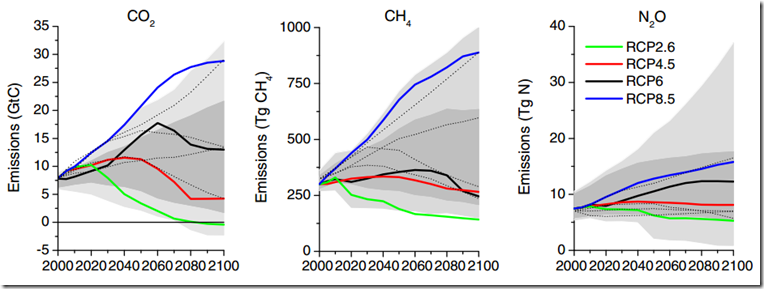
(My bold).  Note that RCP4.5 involves a continual increase of global CO2 emissions up until ~2040, whereas RCP6.0 shows a large increase in emissions until ~2060 (see below, from Figure 6 of van Vuuren et al., 2011)  It is obviously of interest to know the likelihood of staying under the 2°C since pre-industrial target this century without reducing global emissions (note that reducing emissions is not the same as reducing the rate of emissions increase) for another 30 – 50 years.

Figure 6, van Vuuren et al., 2011

The statement is repeated in a bullet point below E.1, along with the reference to where we can find more information in the heart of the report:

Relative to the average from year 1850 to 1900, global surface temperature change by the
end of the 21st century is projected to likely exceed 1.5°C for RCP4.5, RCP6.0 and RCP8.5
(high confidence). Warming is likely to exceed 2°C for RCP6.0 and RCP8.5 (high confidence),
more likely than not to exceed 2°C for RCP4.5 (high confidence), but unlikely to exceed 2°C
for RCP2.6 (medium confidence). Warming is unlikely to exceed 4°C for RCP2.6, RCP4.5 and
RCP6.0 (high confidence) and is about as likely as not to exceed 4°C for RCP8.5 (medium
confidence). {12.4}

My Bold.  Based on my reading,  I think the current state of evidence makes it difficult to agree with the qualitative expressions of probability given for RCP4.5 ("more likely than not") and RCP6.0 ("likely") regarding the 2 degrees target, as well as the "high confidence" given, which I will explain in more depth below.

My interest in this was sparked recently when using a two-layer model with prescribed TCR and effective sensitivities to trace the warming up to the year 2100.  Somewhat surprisingly, I found that for many realistic TCR scenarios, the simulated earth warmed less than 2°C  by the end of the century.  I began to do a scan of the recently released AR5 to find the justification for the scenarios mentioned above.

2. Probabilistic Statements and Confidence

First, let’s discuss what the SPM means by "more likely than not to exceed 2°C for RCP4.5 (high confidence)".  Based on my reading of the Uncertainty Guidance, I believe this should mean there is more than a 50% chance of reaching 2°C by the end of the century ("more likely than not"), and that there is plenty of evidence that is in widespread agreement ("high confidence") about this probability.  Regarding the statement about RCP6.0, "Warming is likely to exceed 2°C for RCP6.0 and RCP8.5 (high confidence)", the "likely" refers to a greater than 66% probability.

Anyhow, since SPM points us to Chapter 12 (and section 12.4 in particular) that’s where I’ll start.  From section 12.4.1.1:

The percentage calculations for the long-term projections in Table 12.3 are based solely on the CMIP5 ensemble, using one ensemble member for each model. For these long-term projections, the 5–95% ranges of the CMIP5 model ensemble are considered the likely range, an assessment based on the fact that the 5–95% range of CMIP5 models’ TCR coincides with the assessed likely range of the TCR (see Section 12.4.1.2 below and Box 12.2). Based on this assessment, global mean temperatures averaged in the period 2081–2100 are projected to likely exceed 1.5°C above preindustrial for RCP4.5, RCP6.0 and RCP8.5 (high confidence). They are also likely to exceed 2°C above preindustrial for RCP6.0 and RCP8.5 (high confidence).

This seems to suggest that for the long-term projections (that is, the warming expected by the end of the century), this is based solely on the CMIP5 model runs.  The observational assessments of TCR (transient climate response) only come into play in so much as that “likely” range approximately matches the 5%-95% range of CMIP5 models.  Notice that the statement of greater than 2°C being “more likely than not” for RCP4.5 is absent right here, despite being present in the relevant portion of the SPM.  So how does that statement find justification in the SPM, and how does it have "high confidence"?

3. On the “More Likely Than Not / High Confidence” RCP4.5 Statement

My impression is that this statement arises based on table 12.3, where 79% of the models produce a warming of more than 2°C under the RCP4.5 scenario.  The high confidence presumably comes from the agreement between the assessed likely  range of TCR estimates and the 5-95% range of TCR in models, but the problem with this becomes obvious when looking at box 12.2, figure 2:

Box 12.2, Figure 2

Note that while the assessed grey ranges roughly match, the actual distributions are largely different.  The CMIP5 models have a mode for TCR > 2 (with a mean of 1.8, per chapter 9), while most of the AR5 estimates show a mode to the left of it.  In other words, just because there is "high confidence" in the 5% and 95% boundaries for CMIP5 projections, this does NOT give a legitimate basis for translating it into confidence about more specific aspects of the CMIP5 projected temperature rise distributions, particularly the "most likely" values (implied by the "more likely than not" statement).  Moreover, our best current evidence suggests the average of CMIP5 models is running too hot (as seen below), so one must be especially careful about making such specific statements based AOGCM results.

In section 12.4.1.2, the report alludes to the higher CMIP5 transient response issue:

A few recent studies indicate that some of the models with the strongest transient climate response might overestimate the near term warming (Otto et al., 2013; Stott et al., 2013) (see Sections 10.8.1, 11.3.2.1.1), but there is little evidence of whether and how much that affects the long term warming response.

This last statement is quite curious.  After all, the report claimed above that the rough matching of the range of TCR estimates with the 5-95% range of CMIP5 TCRs increased confidence in CMIP5 projections of long-term warming, but here the discrepancy in TCRs between estimates and models is dismissed due to lack of evidence of how it affects long-term warming? This seems hard to reconcile with Box 12.2, which notes:

For scenarios of increasing radiative forcing, TCR is a more informative indicator of future climate than ECS
(Frame et al., 2005; Held et al., 2010).

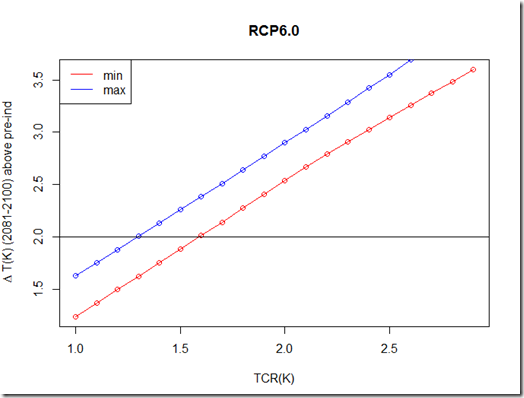
Indeed, this relative importance of TCR for end of century warming is one of the things I talked about in my last post Further investigation using that 2-layer model (script here) produces the following chart of TCR vs. 2081-2100 temperature above pre-industrial: 

While the model is simplified and only uses one mean forcing series (from Forster et al., 2013), it indicates that a TCR less than 1.6 K likely indicates less than 2 degrees of warming by the end of the century for the RCP4.5 scenario.  Again, going back to table 12.3, we see that 79% of the models produce a warming of more than 2°C under the RCP4.5 scenario.  However, by my count, only 8 of the 31 models (26%) have a TCR of less than 1.6K, so this matches up decently with expectations based on TCR (although the picture isn’t quite that pretty, as 2 have TCRs of 1.6K).  Nonetheless, I would suggest that if the true TCR is less than 1.6K, the RCP4.5 scenario is unlikely to produce a warming of more than 2°C by the end of this century (relative to pre-industrial). 

Thus, our question comes down to this – given the best possible evidence, what is the probability that TCR is < 1.6K?  I would suggest it is "more likely than not".  First of all, it appears that the bulk of the AR5 estimates that include a pdf show a most likely value <= 1.6K.  This is despite the fact that (I believe) only Otto et al. include the lesser impact of aerosols assessed in AR5 in their estimate, which would further reduce the estimated likely values for TCR.  Second, it is generally accepted now that the multi-model mean, with its 1.8K TCR, is running on the warm side.  Either way, given the discrepancy between most-likely values in the various estimates, I would downgrade the confidence.

My rewrite of the SPM for this part: "Relative to the average from year 1850 to 1900, global surface temperature change by the end of the 21st century will more likely than not stay below 2°C for RCP4.5 (medium confidence)."    

4. On the “Likely” / “High Confidence” RCP6.0 Statement

Things start out a bit confusing for the "likely"  greater than  2°C statement for RCP6.0, per the following comment under the chapter 12 executive summary notes:

Under the assumptions of the concentration-driven RCPs, global-mean surface  temperatures for 2081–2100, relative to 1986–2005 will likely
be in the 5–95% range of the CMIP5 models

(My italics)  I say that this is somewhat confusing because a 5%-95% range – according to the chapter  – is associated with "very likely", and not simply "likely".  However, we must distinguish between the range of model outcomes and that of real world possibilities, which the authors appear to do as well.  Given that the assessed "likely" range of TCR is approximately as wide as the 5%-95% TCR range of the CMIP5 models, it is clear that some sort of probabilistic downgrade is required (that is, using only 1 standard deviation of CMIP5 model TCR does not properly capture the whole "likely "range of real-world TCRs).  So the authors assess that the "very likely" range of CMIP5 models is only expected to capture the "likely" range of real-world possibilities (Sect 12.4.1.2 again):

The likely ranges for 2046–2065 do not take into account the possible influence of factors that lead to near-term (2016–2035) projections of GMST that are somewhat cooler than the 5–95% model ranges (see Section 11.3.6), because the influence of these factors on longer term projections cannot be quantified. A few recent studies indicate that some of the models with the strongest transient climate response might overestimate the near term warming (Otto et al., 2013; Stott et al., 2013) (see Sections 10.8.1, 11.3.2.1.1), but there is little evidence of whether and how much that affects the long term warming response. One perturbed physics ensemble 
combined with observations indicates warming that exceeds the AR4 at the top end but used a relatively short time period of warming (50 years) to constrain the models’ projections (Rowlands et al., 2012) (see Sections 11.3.2.1.1 and 11.3.6.3). Global-mean surface temperatures for 2081–2100 (relative to 1986–
2005) for the CO2 concentration driven RCPs is therefore assessed to likely fall in the range 0.3°C–1.7°C (RCP2.6), 1.1°C–2.6°C (RCP4.5), 1.4°C–3.1°C (RCP6.0), and 2.6°C–4.8°C (RCP8.5) estimated from CMIP5.

My bold.   (Note that the chapter indicates 0.6°C as the difference between pre-industrial and 1986-2005, so the RCP6.0 range is 2.0°C–3.7°C above pre-industrial, as confirmed in table 12.3). 
 
So, what are the problems here?

First, this seems awfully casual about the divergence between model projections and observed temperatures.  I understand that it may be unclear about how this relates to long-term projections (although several recent observational studies find a lower ECS than most model CMIP5 ECS’s as well), but this should not then translate into "high confidence" in the CMIP5 projections, particularly the lower end of that range.

Second, the assessed "likely" TCR range includes TCR values that would probably keep the RCP6.0 scenario below 2.0°C by the end of the century.  Note that the floor of the RCP6.0 range for CMIP5 is exactly 2.0°C above pre-industrial, which is presumably why the executive summary was able to say warming will "likely" be above 2.0°C for that scenario, but just barely.  Again, the confidence is "based on the fact that the 5–95%  range of CMIP5 models’ TCR coincides with the assessed likely range of the TCR".  But the ranges don’t match exactly, per Box 12.2 again:     

This assessment concludes with high confidence that the transient climate response (TCR) is likely in the range 1°C–2.5°C, close to the estimated 5–95% range of CMIP5 (1.2°C–2.4°C, see Table 9.5).

So the lower end of the "likely" range of TCR is 1.0°C (all evidence) rather than 1.2°C (CMIP5 only).  This would be a rather trivial difference, except that the lower floor for projected "likely" range using CMIP5 for RCP6.0 is exactly 2.0°C, so that lowering this 5% range to reflect all evidence – even if only from 1.2°C to 1.0°C – means probably lowering that projected warming above pre-industrial floor to around 1.7°C (1.0/1.2 * 2.0).  In other words, the "likely" range actually includes values below 2.0°C, and it would be difficult to say that that rise for RCP6.0 is "likely" to be above 2.0°C.***

Moreover, as you can see from my simple two-layer model tests below, a TCR <= 1.4K would mean we would probably see less than 2.0°C in this scenario:

Obviously, there is not much to suggest that the possibility of a TCR <= 1.4K is "unlikely", particularly when examining Box 12.2, Figure 2.  What’s more, the Otto et al. estimates, which are (I think) the only ones listed to use the AR5 aerosol estimates, indicate the "most likely" value is in this range!  So we are left in the rather awkward position that one of the more high-profile studies, using the most up-to-date data, suggests a "most likely" value for TCR that implies less than 2.0°C warming by the end of the century for RCP6.0, but the executive summary says that there is "high confidence" that greater than 2.0°C warming is "likely".

Third and finally, note that the "likely" ECS range in AR5 includes 1.5 K (Box 12.2, fig 1).  Now consider that the "effective forcing" for the RCP6.0 scenario above pre-industrial is 4.8 W/m^2.  This means, that at an ECS of 1.5K, you would only have 1.9°C of warming (4.8/3.7 * 1.5) at equilibrium (which can take several centuries to reach), regardless of the TCR.  Given the time delay to reach that equilibrium, it is probable that any ECS below 2K is unlikely to produce more than 2°C of warming by the end of the century in the RCP6.0 scenario.  Thus, the "likely" statement for more than 2°C in RCP6.0 is again questionable, even if based solely on the AR5 likely range of ECS estimates.

One more thing I want to address is the fact that in table 12.3, 100% of the RCP6.0 model runs produce a temperature rise greater than 2°C, despite 5 of the CMIP5 models having a TCR <= 1.4K.  From what I can tell, FGOALS-g2 (1.4K TCR) and INM-CM4 (1.3K TCR) didn’t participate in the RCP6.0 runs.  For the other three models (GFDL-ESM2G, GFDL-ESM2M, and NormESM1-M), I would have expected (based on their TCRs alone) to see less than 2°C of warming, and can only offer a few possible explanations: a) The ECS values of 2.4, 2.4, and 2.8 for these models are high relative to what one might expect for their low TCR values (failing to touch the lower end of the assessed "likely" range for ECS), and despite the greater importance of TCR, the higher ECS in this case might have pushed them just over the 2C mark, and/or b) these models may have produced an "effective forcing" for the RCP6.0 scenario greater than the 4.8 W/m^2 from the model ensemble.       

My rewrite of the SPM for this part: "Relative to the average from year 1850 to 1900, global surface temperature change by the end of the 21st century are as likely as not to exceed 2°C for RCP6.0 (low confidence)."    

***Note I say "difficult" rather than "impossible", because if the "likely" range include the middle 67% (approximately +/- 1 standard deviation), then excluding a low value from this likely range actually suggests about an 84% probability of it being greater than this value, not simply the 67% required to get to "likely".  However, more discussion / justification would certainly be required about performing a one-tailed test to deem a value "unlikely". 

5. Discussion

While I disagree with these particular statements in the SPM regarding the current best evidence, I find it hard to fault the authors, as I think much of the problem results from the IPCC process.  Essentially, with the projections based almost entirely on the CMIP5 models, and the IPCC unable to present any “novel” science that doesn’t appear published elsewhere (and hence produce new projections), it is hard to incorporate various other estimates of TCR and ECS into these projections.  Moreover, one is forced to consider most (or all) studies regardless of quality and even if using outdated data.  In fact, I think the authors made a wise decision to avoid using the 5%-95% range from CMIP5 as “very likely”, instead downgrading it as “likely” to reflect the spread of estimated TCRs and ECSs.  Unfortunately, this still has implications on the edges (as with the RCP 6.0 lower boundary of 2°C instead of 1.7°C) and center (trying to figure out a “most likely” value for RCP4.5).  Moreover, we have a rather awkward situations where “likely” values of TCR and ECS imply less than 2°C warming for RCP6.0, but we the SPM says that there is “high confidence” in a “likely” diagnosis for more than 2°C warming under RCP6.0.

Overall, I do not envy the job of the IPCC authors, and tend to agree that producing these massive reports for free is probably not the best use of anyone’s time.  It might be better to just create a “living” document such as a wiki, as others have suggested, although I can only imagine the struggles one would come up with in determining the rules for that.

6. Summary

In my opinion, the IPCC summary for policymaker’s overstates both the probability and the confidence in hitting the 2°C target by the end of the century for the RCP4.5 and RCP6.0 scenarios.  This is because:

• The statements about the probability were based primarily upon CMIP5 projections
• Confidence in these long-term projections was primarily justified by the 5%-95% range of CMIP5 transient climate responses (TCRs) matching up with the assessed likely range of TCRs from a variety of other sources, yet
• Where the real-world transient responses began to diverge from models, this was not determined to decrease confidence in the long-term range of projections, and
• Confidence in the 5%-95% range of CMIP5 TCRs was deemed to imply confidence in the “most likely” (50%) CMIP5 projections for RCP4.5, despite the AR5 “all-evidence” assessed TCR having a largely different distribution than that of the CMIP5 TCRs.
• Despite the fact that several assessed “likely” values for TCR imply less than 2°C warming for RCP6.0, it was still determined that there was “high confidence” that greater than 2°C warming was “likely” for RCP6.0
• Despite the fact that several assessed “likely” values for equilibrium sensitivity (ECS) imply less than 2°C warming for RCP6.0, it was still determined that there was “high confidence” that greater than 2°C warming was “likely” for RCP6.0

Relative importance of transient, effective, and equilibrium sensitivities

 

Introduction

I have heard it mentioned that the transient sensitivity (or transient climate response, TCR) is more relevant to climate policy than equilibrium climate sensitivity, and wanted to see the degree to which this is true.  AR4 notes that:

Since external forcing is likely to continue to increase through the coming century, TCR may be more relevant to determining near-term climate change than ECS.

Also, see this very interesting paper by Otto et al., (2013) ERL.  In particular, I wanted to see the relative importance of different types of sensitivity (transient, "effective", and equilibrium) when determining the temperature anomaly in the year 2100 relative to 1850.  For a recap of these types of sensitivities, let’s go back to our simple energy balance model:

C(dT/dt) = F – ΔT*λ

Here, C represents the heat capacity of the system, T represents the surface temperature, F represents the forcing, and λ the strength of radiative restoration.  The TCR refers to the change in temperature in the 1% CO2 increase per year idealized scenario at the time when the concentration doubles, which occurs at 70 years (1.01^70 = 2.0).  Given the large heat sink that is the ocean, there will still be a residual imbalance at the top of the atmosphere after this 70 years.  This means that TCR depends not only on λ, but also on the heat uptake of things like the ocean, which could be represented here in the C term (although note that C varies over time as heat is captured by deeper layers of the ocean, which is why a one-box model is not great for simulating short and long-term transient responses). 

For the equilibrium sensitivity, we also use the 2xCO2 scenario, but this time see how much the temperature changes after radiative equilibrium is reached at the top of atmosphere.  Now, in the idealized situation where λ is unchanging, we can calculate the temperature at equilibrium independent of the heat capacity of the system, as simply ΔT = F / λ.  It is this situation where we use a single-value of λ to calculate ΔT that the ΔT is referred to as "effective sensitivity".  Here, we’ll define λ_250 as the radiative restoration strength from 1850-2100, and ΔT = F_2xCO2 / λ_250 will be our "effective sensitivity".  This differs from ECS in that λ could theoretically change over subsequent centuries, as in Armour et al., 2012.  However, defined this way, ECS is irrelevant for this century’s warming, and such a discussion is more just academic (which is why the distinction between ECS and "effective sensitivity" has been minimized in the past). 

So, in this way, I will technically be comparing the importance of TCR vs. effective sensitivity (EFS), although the latter is sometimes used synonymously with ECS.

 

Method

Here, I will be employing the same two-layer model as in my last post.  Since EFS is determined by λ, it is easy to prescribe in this model.  However, the TCR depends not only on the EFS, but the heat transfer of the ocean as well.  To match the TCR to a target for a given EFS, I fix the "shallow" and "deep" layers at 90m and 1000m respectively, and use a brute force method (ugly, I know) to determine the rate of heat transfer between these layers that will result in this TCR.  From there, I have a model that simulates both the specified TCR and EFS, which I can then use to see the temperature rise from 1850 to 2100 using this model.

I have chosen TCRs of 1.1K, 1.4K, 1.8K, and 2.1K, and EFSs of 1.5K through 4.5K, based on what is feasible/possible for a given TCR.  Again, the adjusted forcings for the RCP scenarios come from Forster et al. (2013). 

Script available here

 

Results

This first graph is for the RCP6.0 scenario:

As you can see, the relatively flat lines (small slope) indicates that given a specific TCR, the EFS has only a small effect on the temperature that might be expected in 2100.  On the other hand, the large amount of space between the different TCR lines, despite only small changes in the magnitude of TCR, indicates that two models can have the same EFS but produce very different magnitudes of warming by 2100 if their TCRs differ. 

To quantify a bit more, the slope of the TCR-2.1 line is 0.16K per EFS, meaning that if the earth had a transient response of 2.1K, the difference between an EFS of 3.0 and an EFS of 4.0 would only produce an extra 0.16K in 2100K.  On the other hand, if we fixed the EFS at 3.0 and instead changed TCR, you can see that an increase between TCR of 1.4K and 2.1K (0.7K) produces a change of the same magnitude (~0.7K) in the expected temperature change by 2100, producing a ratio of 1.0 K per TCR.  A similar difference is found at 2.0 EFS when moving from 1.1K to 1.8K.  This would suggest that it is much more important to pin down the TCR (which has a large impact on this century’s warming), even if EFS remains uncertain, rather than trying to pin down EFS.  I should note, however, that for the low TCR scenario (1.1K), the slope of the line is ~0.34 K per EFS, which is double that at 2.1K.  This is because a low TCR suggests a lower heat capacity of the system, which in turn means a quicker pace to equilibrium, which means a greater importance of EFS. 

For another look, here is the RCP4.5 scenario:

Here, the results are similar to the RCP6.0, although not quite as drastic.  For a given EFS (2.0 or 3.0), the change in 2100 warming is altered by about 0.75 K per TCR (rather than 1.0 K per TCR in the 6.0 scenario).  Part of this is because we only have ~3/4 of the forcing change (4.5 W/m^2 rather than 6.0 W/m^2), so obviously the warming in general by 2100 is decreased.  However, this alone does not explain why the slopes for the TCR-1.1 and TCR-2.1 have increased to 0.4 K / EFS and 0.2 K / EFS respectively.  For that, I suggest that the earlier stabilization of the 4.5 scenario forcing lends a slightly increased importance to the EFS, given the ~30 years it has to move towards that equilibrium prior to 2100.

 

Conclusion

Clearly, TCR seems to be more important that EFS and (definitely more so than ECS) in determining the expected warming by 2100.  I tend to agree that it terms of policy, this suggests more focus should be placed on pinning down the TCR.