Note that by “pause in global warming” I am specifically referring to a near-halt in the underlying low-frequency signal of surface temperatures (not ocean heat content), a signal not influenced by the typical “exogenous factors” of ENSO, volcanoes, or solar activity. This has been recently attempted in Foster and Rahmstorf (2011), from which they conclude that from the “removal” of these three factors via multiple regression they have “isolat[ed] the global warming signal” and that “there is no indication of any slowdown or acceleration of global warming, beyond the variability induced by these known natural factors.” Rahmstorf et al. (2012) proceeds to compare this adjusted temperature evolution to model projections, which I think is particularly dangerous if what you get after this multiple regression approach is not the underlying signal.
Another title for this post could be, “does the multiple regression approach actually reveal the underlying signal”? Or, without spoiling too much, “is the Pinatubo recovery still contributing to the surface temperature trend?” I attempt to test this using two scenarios from a simple energy balance model, with script available here. The model is of the form ( the discrete unit of t is a month):
Which is basically the same as my previous energy balance model, except that because of the multi-decade span I have included an ocean diffusion term, which just transfers 50% of the mean TOA radiative imbalance of the year to below the mixed layer, and I’ve separated out V as the flux into the mixed layer from deeper ocean to distinguish it from a radiative forcing. It is radiatively forced by a linear “anthropogenic component”, volcanic activity, and solar activity. Variation is also induced via ENSO, and, in the case of scenario 2, a 60-year oscillation, represented by a heat flux from the lower ocean into the mixed layer. Since we will force this model using the same datasets/indices that we use to remove the influence, and we don’t introduce any other noise, I consider this a best-case scenario for the multiple regression approach.
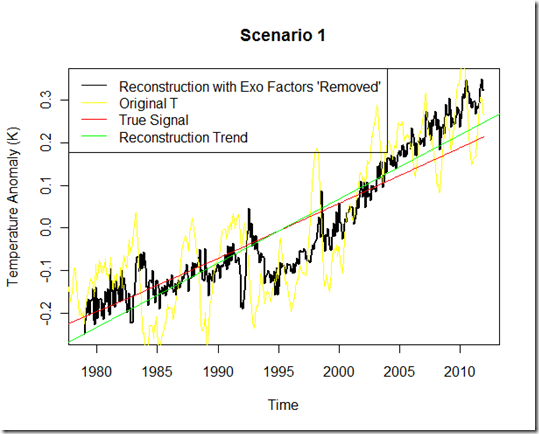
First, we have scenario 1. This has only the three “exogenous” factors and the linear anthropogenic forcing. The red line represents the global warming ”signal”…that is, the model run without the additional three factors. It starts in 1955, and thus takes a bit of time to react due to the ocean terms, but as you can see from 1979 on the “signal” is pretty much a straight line.
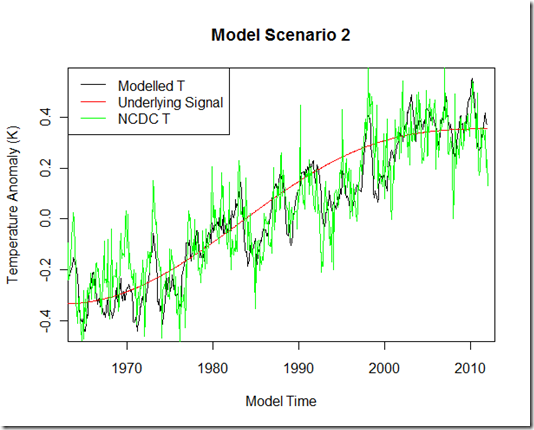
Next is scenario 2. Here again, I have included all the factors from scenario one, but I have also include a 60-yr oscillation on top of the anthropogenic forcing for the underlying low-frequency signal, which basically increases the warming trend from 1980-1995, but counteracts much of the anthropogenic forcing from 2000 to present to produce a virtual “pause”. I have included NCDC temperature anomalies to show that the modeled temperature result is pretty realistic, although with the amount of tunable parameters here (mixed layer heat capacity, ocean diffusion, radiative restoration strength) I will not be patting myself on the back for the match.
Next, I use the output from the modeled temperature and run the multiple regressions similar to the FR11 method (I do not include a Fourier series as the model contains no annual cycle). Ideally, if this method were perfect, I should be able to recover the red signal from the black.
First, we have scenario 1. For the solar and volcanic lags and “influence”, I found largely different fits when using the modeled T than FR11 found when using actual temperatures. Perhaps this is a sign that a more realistic model would yield better results for the multiple regressions, although I ‘m not sure how using a model with more complexities introduced would make it easier to pick out the influence of the different components.
The original modeled T is in yellow, whereas the new reconstructed/adjusted temperature set, with the exogenous factors “removed”, is in black. Here, we see a reduction in the variability from yellow to black, but the green line representing the slope from this reconstruction has actually increased and is greater than the true “red” signal. As such, I’m not sure the trend of black “adjusted temperatures” better represents the true signal (red) at all!
But the real test is scenario 2. Here we have an actual pause in the underlying signal “red”, and we would hope that the multiple regression method, having removed exogenous influences, would still leave that true signal intact.
As you can see, this approach yields an extremely poor “reconstruction”. One might even conclude that there was little slowdown in the warming since 2000 (trend of .178 K/decade in the reconstruction) if looking at this result, despite the fact that the true signal shows a near-halt over this period (trend of 0.037 K/decade)!
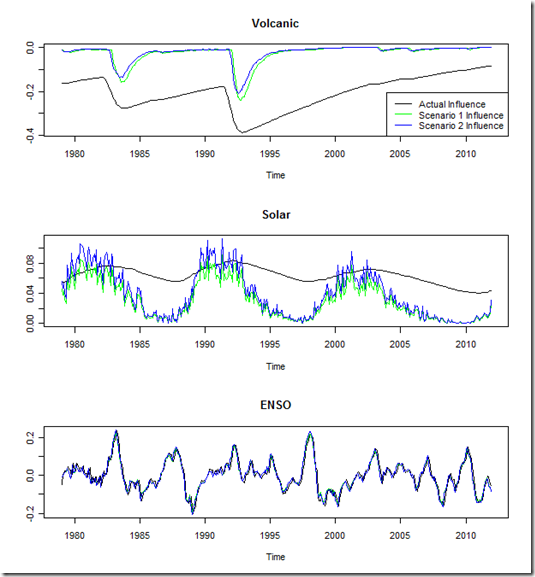
So, where did this multiple regression approach go wrong? We can diagnose this by comparing the influence determined from each regression to the actual influence in my energy balance model (determined by running the model with only that component).
First, I will note that the influence of ENSO is diagnosed extremely well. This is no doubt due to using the same index with no noise for both the forcing and determining the influence, while also noting the high-frequency and relatively high magnitude of the influence. A more complex model, or the real-world, would not likely lead to such results, but remember we’re looking at a near “best case” scenario here.
Second, we see that the solar influence is largely over-estimated. As I’ve indicated before, I think that it is hard to pick out the solar signal among the noisy data, and so given the slow-down in surface temperatures corresponding with a recent dip in solar activity, a regression model might conclude that this has a bigger impact than it actually does.
However, the biggest error here comes from an underestimate of the volcanic influence. Whereas the regression “removal” essentially sees the influence of the exogenous factor end after the forcing ends (plus whatever lag is diagnosed), the energy balance model used here shows a continuing influence through the last decade as part of the recovery. In fact, this in itself contributes about a 0.1K/dec trend to the most recent decade in the model!
Personally, I am not aware of any studies suggesting that recovery from the Pinatubo eruption might still be contributing a positive trend in 21st century temperatures. The question that arises, then, is whether this effect is just an artifact of my unrealistic model? Unfortunately, not many CMIP5 groups performed a historical, volcanic-only simulation, and the one I looked at only goes through 2005. Furthermore, the volcanic-only forcing simulations still include internal dynamics such as ENSO, so it is not that easy to isolate. Nevertheless, here is what I found for the GFDL-ESM2M run (script here):
I would say the results here are still ambiguous. The red represents a Lowess smooth, and that at least tentatively suggests an increasing trend from 2000 to present from the Pinatubo recovery, if we were to assume that that peak around 2000 and dip in 2002 were internal ENSO dynamics. Sadly, there are no more volcanic-only runs in the CMIP5 archive for this model to test that idea. There are a couple other models in the archive that have multiple runs for this, I will see if they reveal anything extra. I would also like to test the multiple regression method with different types of noise added to see how that impacts the performance as well.
Conclusions
From what I can tell, in this case, the multiple regression approach used by Foster and Rahmstorf (2011) [and Lean and Rind (2008), although I haven’t investigated the specifics of that paper] can produce misleading results, even failing to recognize a pause in the underlying signal. In those cases, the “reconstruction” can be a worse representation of the true signal than the original, unadjusted results, and should not be used to test projections. Of course, in this particular case, much of it seems to stem from a lingering effect of the Pinatubo recovery into the 21st century, which I am currently skeptical exists in the real world.




Very nice Troy. It has been my opinion for some time that ocean response time is such that an appropriately specified model should reveal a longer “memory” of an event like Pinatubo.
Aurthur Smith set up a model for forecasting a couple of years ago based on a rough approximation of F&R which he has been using for GISS predictions (2012 prediction contained in this post). I reproduced his model using his coefficients and plugged in the 2012 values for MEI and ssn. Aurthur based his 2012 prediction (mean 2012 GISS of 0.65C) on projections for MEI values which actually came in a little higher IIRC. Plugging in the acutal values for 2012 I calculate a GISS prediction of 0.68C vs observed mean 0.53C for 2012 GISS (using 0.44C for Dec). The trend slope in Arthur’s model is about 0.15C per decade.
Comment by Layman Lurker — January 26, 2013 @ 11:31 am
Thanks LL. I agree that Pinatubo should have a longer recovery time than assumed by the multiple regression model, but I am dubious whether this effect lasts quite as long as in my simple model above. According to the document I have, there should be four models that ran the volcanic-only experiment in the CMIP5 archive, but I could not find the GISS-EH or GISS-ER ones on ESGF so far. I looked at the GFDL-ESM2M run, with the mixed results above, and found 5 runs from CSIRO-Mk3.6 as well. The mean 21st century trend in that ensemble is around 0.04 K/decade (and 4 of the 5 had a positive trend, with 3 of the 5 being 0.08 K/Decade or above), but the model seems to greatly overestimate that decade-long variability, such that the SD of those 5 run 21st century trend is 0.16 K/Dec which again leaves the result quite ambiguous.
Comment by troyca — January 27, 2013 @ 5:30 pm
Of course, in this particular case, much of it seems to stem from a lingering effect of the Pinatubo recovery into the 21st century, which I am currently skeptical exists in the real world.
I have been looking a little more closely at comparisons of enso, sst, and solar (ssn). In general SST begins to track solar part way up the ramp and lose track shortly after the peak. During the early and late periods of the solar cycle (low SSN levels) SST tracks ENSO. See this example using solar cycle 10. it seems that as SST warms, the level of ssn at which SST begins tracking tends to get higher leaving a much smaller segment near the peak where SST/SSN correlation is evident and ENSO correlation becomes predominant. Recently, SST is still at or near it’s highest levels and solar has begun to drop. In all cycles, SST tracks either SSN or ENSO (and sometimes both). For the last two solar cycles, SST has really not tracked solar at all (perhaps a little near the cycle peak) – but has tracked ENSO very closely. Here is the segment for cycle 23.
This looks like evidence of ocean energy imbalance within the solar cycle. High levels of SSN correspond with absorbtion of solar energy (SST tracks solar). Low levels of SSN correspond with release of solar energy (SST tracks ENSO). The level of SSN at which energy balance is achieved is related to the SST level. An Increase in SST implies an increase in SSN to maintain energy balance. if peak SSN fails to reach the energy balance level, then SST will track ENSO throughout the cycle but not SSN.
When SST tracks ENSO at the back end of the cycle it is more of slow downward drift rather than the sharp drop which would occur if it mirrored the solar forcing. As a result of the longish memory of the initial solar impulse, in the transition to the next cycle sst must ‘step’ up . This to me seems consistent with the impulse / response type of relationship you saw expressed with volcanic influence.
To illustrate that ENSO stages are related to the solar cycle, one can overlay the segments of ENSO corresponding to the solar cycles, and express the ENSO values in the ‘solar cycle’ domain. Here are the ENSO segments during cycle 22 and 23 compared in the solar cycle domain.
Comment by Layman Lurker — January 27, 2013 @ 11:21 pm
Just found this buried deep in the SPAM bin, sorry for missing it earlier (WP seems to hate more than a single link per comment)!
Comment by troyca — February 7, 2013 @ 7:17 am
[…] 2013/01/25: TMasters: Could the multiple regression approach detect a recent pause in global warming… […]
Pingback by Another Week of GW News, January 27, 2013 – A Few Things Ill Considered — January 29, 2013 @ 2:06 pm
I’ve put this up at real climate.
http://www.realclimate.org/index.php/archives/2013/02/2012-updates-to-model-observation-comparions/comment-page-2/#comment-319650
Comment by Armando — February 13, 2013 @ 3:51 am
OK, I’m impressed.
While I think F&R is a step in the right direction, I’ve had my own concerns for a while (some of which I’ve argued over at Tamino’s):
1. Using the exogenous factors to address the differences between surface series, when we know those differences are dominated by coverage bias is suboptimal. I’m mainly working on the coverage bias issue at the moment.
2. Using a simple delay rather than an exponential or more sophisticated lag misses the delayed effect of the volcanoes, which happen to be on the cooling slopes of the solar cycle, leading to considerable inflation of the solar term and underestimation of the volcano term. This overlaps with your lag issue. Rypdal (2012) noted the problem.
I’ve tried to address this in two ways in my analysis here: http://www.skepticalscience.com/16_years_faq.html
Both the method and the results are a bit more conservative than the original F&R analysis – 2 fewer params. But I’m not entirely satisfied – see comment #3. It would be interesting to see if my analysis survives your test. Here’s a brief outline of that I’ve done:
The first approach is to tie the volcanoes and solar together as forcings and fit a single exponential response term instead of a delay. The number of params is reduced by 2. The resulting volcano term is much bigger and the solar term smaller. While the regression coefficients are very well determined, the lag is not. (The best lag term is an exponential with a time constant of 14 months.)
The second is to use a 2-box+enso model (e.g. Rypdal 2012), fitting all the forcings. In this case the impulse response is roughly 0.1exp(-t)+0.6exp(-t/30)
t in years – you’ll be interested in the result of convoluting that with the volcano forcing. That’s a dramatically slower response, and is also considerably slower than Hansen’s response function in the 2011 Energy Imbalance paper. It gives pretty similar projections to 2100, but would mean that (as you suggest) we’re still seeing some Pinatubo recovery now (~0.01-0.02C/decade over the 1997-2013 period).
However in the second case the response function is almost entirely constrained by the very uncertain forcings rather than the volcanoes, so this is also unsatisfactory.
If the problem is tractable (which is not guaranteed), then using the 130 year data is the way to go. My next idea is to model the temperatures as an unknown smooth function (because the anthro forcings vary slowly) plus exponential lagged volcano+solar.
The sort of test you’ve devised here will be key to determining whether the results are meaningful or not. The other test I’ve thought of trying is combining the results with a range of lags using model likelihoods as weights, to try and get a handle on the uncertainties. However that’s going a bit beyond my formal stats knowledge. Any thoughts on that would be very welcome.
(p.s. congrats on the paper)
Comment by Kevin C — February 14, 2013 @ 2:13 am
Thanks Kevin. Indeed, I would be interested in testing those improvements on my simple model above, as I think combining the solar+volcanic into a single forcing series and using a model that allows for longer tails on larger forcings should serve to correct some of the primary issues I mentioned. Do you have any code (or even pseudo-code) of your algorithm that I could use to jump-start this work (alternatively, hopefully my script is straight-forward enough for my model you could also give it a whirl)? Another test would be to download those GISS-ER natural forcing only runs (and take out the Nino3.4 region as well), impose some sort of artificial underlying signal, and see how well these methods recover that underlying signal (granted, this would fail to take into account the impact of this underlying signalon TOA imbalance, but if the signalis low frequency it should not affect those higher frequency variations).
Comment by troyca — February 14, 2013 @ 8:18 am
I’ll get my code to you. I think you have access to my email from this post? If so drop me a message.
My 2-box response function above contained an error, I normalise the exp’s, so the second term needs dividing by 30, i.e.: 0.1exp(-t)+0.02exp(-t/30)
You also set me pondering on whether we can set a bound on the effect of Pinatubo on recent trends, and I think I see a way. Assuming no really funky response function (e.g. a sigmoid), then the greatest effect we can have on recent trends would be a 20 year ramp function. The integral of this function will roughly equal the TCR (since 20 << 70years). If we allow a maximum TCR of 2 C/(CO2x2), or 0.55 C/(Wm-2) in line with the most sensitive CMIP3 models, then the biggest response function we can have is 0.055*(1-t/20) (0<t<20). Convolute that with the volcano forcing, e.g. from GISS RadF.txt and you get a upper bound on Pinatubo temperature impact.
(The strat-aerosol forcing seems to be ~-20x the value is tau_line.txt. Isaac Held uses a similar value. The CMIP-5 forcings from Potsdam are unaccountably about half that size, and I can't get sensible results with them.)
Comment by Kevin C — February 17, 2013 @ 7:36 am
Troy,
A pretty definitive demonstration.
It doesn’t affect your findings, but I would be interested in understanding why you chose such an idiosyncratic version of energy balance.
Paul
Comment by Paul_K — February 18, 2013 @ 11:10 pm
Thanks Paul. This model was partly inspired by that of Lin et al., 2010, http://www.atmos-chem-phys.net/10/1923/2010/acp-10-1923-2010.pdf, although obviously there are significant differences and mine is simpler. Essentially, to use the typical energy balance model without a deep-ocean “heat transport coefficient” would involve increasing the mixed-layer heat capacity for a realistic multi-decade response, but this in turn would overdampen the short-term monthly responses. I wanted to maintain the concept of transport between the mixed layer and the deeper ocean being proportional to the TOA radiative balance on some scale, but to simply assume that some percentage of the monthly TOA imbalance is transported to the deeper ocean would seem to assume too quick of a heat transport process. I’m sure there are better models for this out there, but I thought this one seemed simple enough without being “too simple”. I would certainly be interested in thoughts on improving it (there’s likely a better one already out there in the literature)…
Comment by troyca — February 19, 2013 @ 9:20 am
From a statistical point of view, it isn’t surprising that a linear model gives a misleading result if the underlying trend is non-linear. Statistical analyses are only as good as the assumptions on which they are based, and whether an analysis is reasonable depends on the reasonableness of their assumptions. One guide to this is Occam’s razor, which suggests that we should not use a model that is more complicated than necessary to explain the data (i.e. if we have two models that explain the data essentially equally well, we should prefer the more simple). Occam’s razor perfectly well justifies the conclusion that “there is no indication of any slowdown or acceleration of global warming, beyond the variability induced by these known natural factors.”. R&F show that there is no need to invent an exogenous cause for a slow down, as the observations are adequately explained by a linear trend (which is roughly you would expect from the enhanced greenhouse effect) and short term variability due to known factors. This seems to me to be in accord with usual statistical practices.
To take this to the extreme, rather than a simple oscillation, consider that an astrologer might come up with an mathematical argument based on the movement of planets that explained the existing observations exactly. No statistical analysis could be reasonably expected to isolate this *if it actually were the underlying signal*; the only difference between this and the 60-year oscillation is essentially the complexity of the assumptions. We would not accept the astrologers model because it has too many parameters for the amount of data available, but then again, can we justify a 60-year oscillation either? Essentially the answer is no, because (for a “pause” of 16 years or less), a linear model plus known sources of variability explains the observations well enough from a statistical perspective.
From a statistical point of view, the question would be “is there statistically significant evidence for the existence of a pause in the underlying rate of warming?”. The obvious null-hypothesis for this question is that the rate of linear warming has remained constant, and that the apparent pause is explainable by random variability. This is essentially the test that F&R have performed, and the answer is “currently no”.
I think it is also possible that too much is being read into ““isolat[ed] the global warming signal”, as a statistician I would read this as meaning “isolated the expected global warming signal implied by the physics” rather than “isolated the true effect of the anthropogenic influence on climate”, simply because statistical methods fundamentally cannot prove anything (disprove perhaps, or argue about the level of support from the observations, but that is about it). I read this as simply meaning that the signal isolated agrees with what we know from the physics; but it is the physics that is the justification, not the statistics.
Don’t get me wrong, testing the limitations of statistical approaches is something I wholeheartedly approve of, however I don’t think this analysis casts much doubt on the statistcal aspects of F&R, but is a useful caveat on over-interpreting their results.
P.S. Have you asked Tamino for his view?
Comment by dikranmarsupial — February 20, 2013 @ 5:11 am
Dikran: I think you’ve missed the key point here. As you point out, the F&R calculation (and mine too) assumes a linear underlying trend. However if you give it data with a non-linear underlying trend F&R does not reproduce the underlying trend.
The calculation works in the hope is that the parameterisation is parsimonious enough that it can’t create linear trends from a non-linear one, and so will produce a reasonable result even when the underlying trend is non-linear. Troy’s analysis suggests that that hope is ill-founded. As a result, if the underlying trend is not linear there is no guarantee that F&R will tell us.
Comment by Kevin C — February 20, 2013 @ 6:37 am
Why should the F&R calculation give the correct result if the underpinning statistical assumptions are incorrect?
Say we went to a quadratic model instead, and that gave acceptable results. Then somebody could point out that it doesn’t give the correct answer if the result is a cubic. We could then make a cubic model, and someone point out it gives misleading answers with a quartic. The question is, is there a good reason to think that the underlying behaviour actually is a quartic (answers on a post card to Dr Roy Spencer, I’m sure he would be amused ;o). No matter what model you use (unless it is a universal approximator), it will always be possible to construct a scenario where it gives misleading results.
The linear model is essentially a bit like a Taylor series expansion of the actual underlying behaviour, it will pretty much always give a misleading result if a first order Taylor series expansion is an inadequate approximation. However, moving to a more complex model raisies the problem of over-fitting, such that it might extract a non-linear signal where the underlying behaviour is actually linear. Sadly there are no free lunches.
The task in statistical modelling is to chose a model complexity that is well supported by the observations (rather than just giving a good fit to the training sample), so as Occam’s razor suggests, if you want to move to something more complicated than a linear model, you need to be able to provide statistical justification for the added complexity.
There are no guarantees of this sort for statistical models, statistics would be a much easier topic if there were.
Comment by dikranmarsupial — February 20, 2013 @ 7:02 am
DM,
Your points about over-fitting and the F&R method giving misleading results if the underlying trend is non-linear are those that detractors of the method have been making for some time (particularly at The Blackboard). Given that, I’m not sure how this statement follows:
F&R have shown that if you assume “no slowdown” (a linear underlying increase), you will get “no indication of any slowdown.” This demonstration shows that even if there IS a “slowdown” in the underlying signal (flattening in recent temperature trends) you will STILL get “no indication of any slowdown”. If that is the case, the F&R can hardly be relied upon to accurately determine whether there has been a real “slowdown” or not.
From a physics perspective, I do not think that “the observations are adequately explained by a linear trend…and short-term variability due to known factors.” At the very least, the F&R methodology seems to overweight the solar influence, and fails to capture any temperature recovery from Pinatubo past 1995, which exists in both simple energy balance models and volcanic-only GCMs (the question is how far such a recovery lasts into the 21st century). Moreover, there are some indications of a LF oscillation (obviously this is a contentious issue being debated, with Isaac Held recently posting on this with respect to Booth et al. on the AMO), or, if not that, potentially aerosols, as competing explanations for the recent slowdown beyond ENSO+solar+volc.
As Kevin C said, F&R may be a reasonable first step to get a rough idea of how ENSO, volcanic and solar activity might influence recent temperatures. But I would not put too much weight on a reconstruction of the underlying signal, nor the actual influence of these variables…particularly when trying to determine whether the recent “slowdown” is better explained by ENSO+volc+solar alone, or aerosols and/or a LF 60-yr oscillation plays an important role. Perhaps this is what you mean by it being “a useful caveat on over-interpreting their results.”
He noted he is a aware of it on an RC post we both commented on, and mentioned he may do a post of his own on it.
Comment by troyca — February 20, 2013 @ 8:20 am
The point I am trying to make is that I don’t think F&R is intended to establish that there has been no slow down, but instead that the observations are adequately explained (statistically speaking) without having to introduce one. This is a perfectly natural thing to do from a statistical perspective, as it is essentially what frequentist hypothesis testing does. I can see why this might be unappealing from a physics point of view (and indeed why I, being a statistician, am more convinced by phsyical models than statistical ones), but it should be remembered that the Foster is a statistician, so it should be expected that he should take a statistical approach.
Rather than taking an hypothesis testing approach, an alternative would be to compare models (I would use Bayes factors to do this, but there are also frequentist approaches), but to do that you do need to build a model that includes the explanatory variables giving rise to the non-linearity. These methods take Occam’s razor into account in that they include a penalty on the complexity of the model, so a more complex model will only be chosen if the improvement in the fit to the observations is sufficient to justify the added complexity. For example, one could compare a linear+noise model of temperatures over the temperatures since 1979 with Dr Spencer’s quartic (quintic?) plus noise “stricly for entertainment purposes” model. The reason a statistician would not choose the quartic model is that there is insufficent data to reliably estimate all of the parameters of the quartic model, but there is for the linear model (i.e. the trend is statistically significant). If someone wants to establish that there *may* have been a slowdown, on a statistical basis, they need to demonstrate that there is a non-linear model that is adequately supported by the available data. Statistically speaking (hypothesis test) if they want to assert there HAS been a pause, they need to demonstrate that the observations effectively rule out the possibility that there hasn’t been one (which F&R demonstrates cannot be done at the present time). There shouldn’t be different standards of evidence for one side of the discussion than for the other.
I have looked at the issue of change-point detection on these data in the past (although I am not ready to publish anything at the moment), but from what I have done so far, the evidence for a pause is not statistically significant (yet).
I don’t think it is really fair to criticise the physical interpretation of the F&R linear model without also applying the same criticism to the 60-year cycle model, for which as far as I can see the phsyical evidence is highly equivocal.
Comment by dikranmarsupial — February 21, 2013 @ 1:12 am
[…] I posted on the multiple regression method – in particular, the method employed in Foster and Rahmstorf (2011) – and how, when […]
Pingback by Could the multiple regression approach detect a recent pause in global warming? Part 2. « Troy's Scratchpad — February 20, 2013 @ 9:21 pm
[…] Part 1 […]
Pingback by Could the multiple regression approach detect a recent pause in global warming? Part 3. | Troy's Scratchpad — February 23, 2013 @ 12:22 pm
[…] of variation on the global surface temperature (figure created by Skeptical Science). [Recent reanalysis of this shows that one should not use these results for predictive modeling, but I present this […]
Pingback by Surface temperatures are the result of multiple forcing factors – Global warming did not stop in 1998 | Unity College Sustainability Monitor — March 28, 2013 @ 10:05 am
[…] has been a while since I posted the first three parts of a series on whether using multiple linear regressions to remove the solar, volcanic, […]
Pingback by Another “reconstruction” of underlying temperatures from 1979-2012 | Troy's Scratchpad — May 21, 2013 @ 8:26 am
[…] 21/02/2013: Troy Masters is doing some interesting analysis on the methods employed here and by Foster and Rahmstorf. On the basis of his results and […]
Pingback by Skeptical Science Folly: Video Based On Flawed Rahmstorf & Foster Paper Disappears! — June 13, 2013 @ 5:04 am
Not to sound presumptuous but there is one thing that your simulation does not explain – once you assume one extra ocean oscillation (with no physical base whatsoever, but let’s play on this direction for the moment) – wouldn’t that extra ocean influence show in a very DIFFERENT way in the way the ENSO index results look? (and of course again skipping the fact that any such oscillation should be somehow extra-visible in a decent PCA of the signal).
Oh, and regarding the Pinatubo long-term effects – Hansen, James, et al. “Earth’s energy imbalance and implications.” Atmos Chem Phys 11.24 (2011): 13421-13449.
Comment by nuclear_is_good — June 13, 2013 @ 2:23 pm
Nuclear,
I’m not sure that this simulation is attempting to “explain” anything. What is shows is for the case where the underlying trend sharply decelerates near the beginning of the 21st century, the F&R method will incorrectly diagnose this underlying trend.
From what I can tell, your contention is that if there was some low frequency ocean effect, this would necessarily show up in the ENSO index? Perhaps, but I don’t know specifically what you are suggesting … it doesn’t seem to me that a LF oscillation with a global SST of amplitude 0.1-0.2 C would necessarily be obvious in the small Nino3.4 region where the SST variations are a magnitude larger. Not that I am tied to a LF ocean-related oscillations for the potential cause of a recent deceleration either, but I’m also not sure why you consider the possibility so absurd…while the cause is still debatable, my understanding is that various spectral analyses on global temperature series indicate significant power at these lower frequencies. Moreover, the latest reason I seem to be hearing for the recent pause is “more efficient ocean heat uptake”…if that is this case, isn’t it possible that there were periods of “less efficient ocean heat uptake” in the past?
I am indeed aware of the Hansen paper (I believe I mentioned this in the comments at RC when discussing these results some months agao, and Kevin C mentioned it in his SkS article). It is not surprising that he got a long response given his one-box model and large sensitivity. However, prior to my writing of this series, I cannot recall anyone using that tiny portion of the paper in response to the FR11 results, nor do I recall anybody suggesting that volcanoes (among other natural forcings) contributing a substantial *warming* trend to the most recent decade+. If you have any such references, I would be grateful if you would share them, as we’re nearly done writing up this paper and such background would be helpful…
Comment by troyca — June 14, 2013 @ 11:36 pm
[…] of variation on the global surface temperature (figure created by Skeptical Science). [Recent reanalysis of this shows that one should not use these results for predictive modeling, but I present this […]
Pingback by Surface temperatures are the result of multiple forcing factors: Warming has not stopped | The Environmental CenturyThe Environmental Century — March 27, 2015 @ 12:39 pm
[…] of variation on the global surface temperature (figure created by Skeptical Science). [Recent reanalysis of this shows that one should not use these results for predictive modeling, but I present this […]
Pingback by Warming has not stopped: Surface temperatures reflect multiple forcing factors | The Environmental CenturyThe Environmental Century — March 27, 2015 @ 12:51 pm